Bài Tam Giác

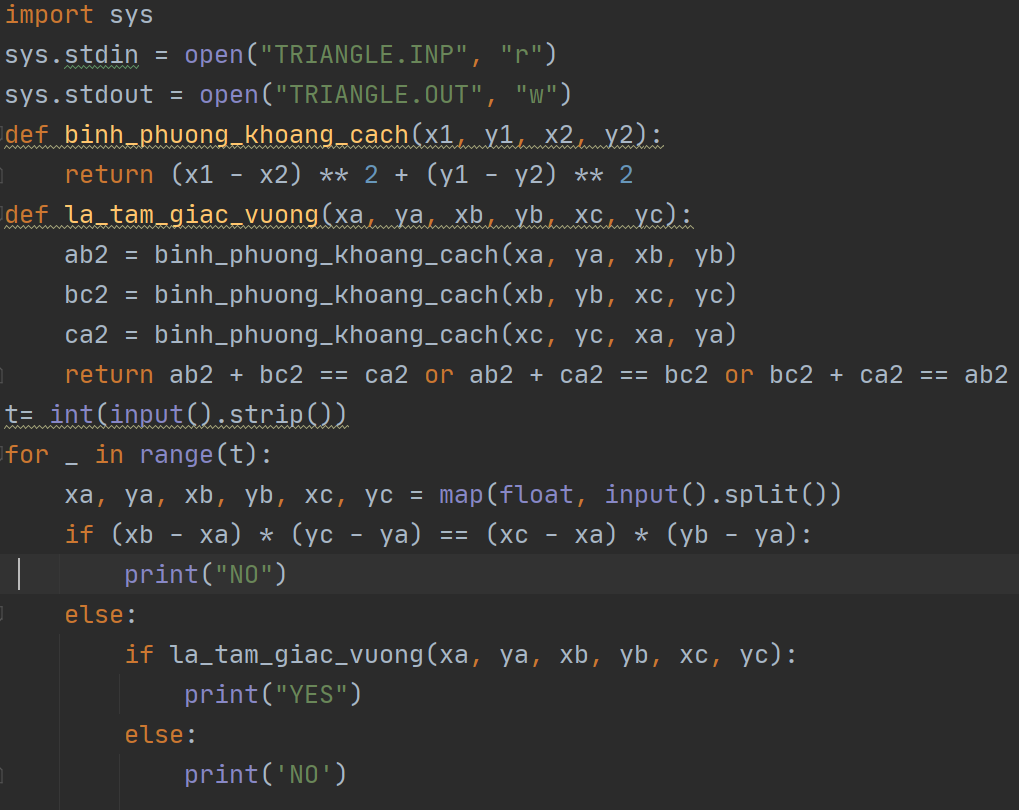
Biểu thức (xb-xa)*(yc-ya) == (xc-xa)*(yb-ya) là một công thức kiểm tra tính thẳng hàng của ba điểm A, B, C trong mặt phẳng tọa độ Oxy. Nó cho biết liệu ba điểm A(xa, ya), B(xb, yb), C(xc, yc) có cùng nằm trên một đường thẳng hay không.
Giải thích chi tiết:
Tọa độ điểm:
Trong biểu thức, các chữ cái ‘x’ và ‘y’ đi kèm với các số (như xa, ya) là tọa độ của các điểm trong hệ trục tọa độ Descartes.A = (xa, ya) là tọa độ của điểm A.
B = (xb, yb) là tọa độ của điểm B.
C = (xc, yc) là tọa độ của điểm C.
Vectơ:
Các phép trừ như (xb-xa) biểu thị độ chênh lệch tọa độ theo phương ngang (trục x), tương đương với thành phần x của vectơ AB. Tương tự, (yc-ya) biểu thị độ chênh lệch tọa độ theo phương thẳng đứng (trục y), tương đương với thành phần y của vectơ AC.
Kiểm tra tính thẳng hàng:
Nếu ba điểm A, B, C thẳng hàng, thì vectơ AB và vectơ AC sẽ cùng phương (cùng hướng hoặc ngược hướng).
Điều kiện để hai vectơ cùng phương là tích của các thành phần tương ứng của chúng bằng nhau, sau khi đã nhân chéo. Hay nói cách khác, tích chéo của chúng bằng nhau.
Khi nào biểu thức này bằng nhau?
Nếu (xb-xa)*(yc-ya) == (xc-xa)*(yb-ya) thì ba điểm A, B, C sẽ thẳng hàng.
Nếu biểu thức này không bằng nhau, ba điểm A, B, C sẽ tạo thành một tam giác và không thẳng hàng.