Bạn đang tìm kiếm tài liệu ôn thi Học sinh giỏi (HSG) Tin học cấp THCS chất lượng, bám sát cấu trúc đề thi thực tế? Bộ Đề thi Học sinh giỏi Tin học THCS Huyện Tân Phước năm học 2021–2022 chính là tài liệu vàng giúp học sinh rèn luyện tư duy thuật toán và bứt phá điểm số trong các kỳ thi sắp tới.

Cấu Trúc Đề Thi HSG Tin Học THCS Tân Phước 2021–2022

22-De-Thi-Hoc-Sinh-Gioi-Tin-Hoc-THCS-Tan-Phuoc-2021–2022-Kem-Loi-Giai-Link-Tai-PDF

Đề thi được thiết kế nhằm đánh giá toàn diện kỹ năng lập trình, tư duy logic và khả năng tối ưu thuật toán của học sinh lớp 8, lớp 9 với các dạng bài từ cơ bản đến nâng cao:

• Bài 1: Xử lý số học & Tính toán cơ bản – Kiểm tra kỹ năng sử dụng vòng lặp, câu lệnh điều kiện và các phép toán chia lấy phần nguyên/dư.

• Bài 2: Xử lý Chuỗi & Ký tự – Bài toán đếm ký tự, tách từ, đảo ngược hoặc kiểm tra chuỗi đối xứng (Palindrome).

• Bài 3: Mảng 1 chiều & Thuật toán Tối ưu – Tìm sub-array, đếm phần tử thỏa mãn điều kiện hoặc bài toán sắp xếp/tìm kiếm.

• Bài 4: Bài toán Tư duy & Thuật toán Nâng cao – Đòi hỏi học sinh biết áp dụng kỹ thuật duyệt, quy hoạch động đơn giản hoặc tối ưu độ phức tạp thời gian $O(N)$.

🟢 ĐÁP ÁN BÀI 1: SỐ NGUYÊN TỐ VÀ ƯCLN

1. Phân tích đề

Cho hai số nguyên dương:

Yêu cầu:

a) Tìm các số nguyên tố từ A đến B

Ví dụ:

Các số nguyên tố là:

b) Tìm ƯCLN của A và B

2. Phần a — Kiểm tra số nguyên tố

Số nguyên tố là gì?

Một số nguyên tố là số:

• Lớn hơn 1
• Chỉ chia hết cho 1 và chính nó.

Ví dụ:

Không phải số nguyên tố:

Cách kiểm tra số nguyên tố

Ta có thể thử chia n cho các số từ 2 đến √n.

Tại sao chỉ cần đến √n?

Nếu:

thì ít nhất một trong hai số a, b phải:

Ví dụ:

Ta chỉ cần kiểm tra đến:

Hàm kiểm tra nguyên tố

def la_so_nguyen_to(n):
    if n < 2:
        return False

    for i in range(2, int(n ** 0.5) + 1):
        if n % i == 0:
            return False

    return True

Giải thích

Nếu:

thì chắc chắn không phải số nguyên tố.

Thử các ước từ 2 đến √n.

Nếu:

thì n chia hết cho i, nghĩa là n có ước khác 1 và chính nó.

→ Không phải số nguyên tố.

3. Duyệt từ A đến B

Ta dùng:

Vì range() không lấy giá trị cuối nên phải dùng B + 1.

Ví dụ:

sẽ duyệt:

Sau đó kiểm tra từng số:

4. Phần b — Tìm ƯCLN

Có nhiều cách tìm ƯCLN.

Cách rất quan trọng trong lập trình là thuật toán Euclid.

Công thức:

Lặp lại cho đến khi:

Khi đó:

Ví dụ UCLN(10, 25)

Ta có:

nên:

5. GIẢI Code hoàn chỉnh Bài 1

def la_so_nguyen_to(n):
    if n < 2:
        return False

    for i in range(2, int(n ** 0.5) + 1):
        if n % i == 0:
            return False

    return True


def ucln(a, b):
    while b != 0:
        a, b = b, a % b

    return a


A = int(input())
B = int(input())

# Tìm các số nguyên tố từ A đến B
for i in range(A, B + 1):
    if la_so_nguyen_to(i):
        print(i, end=" ")

print()

# Tìm UCLN
print(ucln(A, B))

Kết quả:

Đúng với ví dụ trong đề.

6. Độ phức tạp Bài 1

Có:

số cần kiểm tra.

Mỗi số kiểm tra đến căn bậc hai của nó.

Do đó độ phức tạp khoảng:

Với B < 100 thì cực kỳ nhanh.

Thuật toán ƯCLN

Thuật toán Euclid có độ phức tạp:

Đây là cách tìm ƯCLN rất hiệu quả.

🟠ĐÁP ÁN BÀI 2: ĐÁNH SỐ CÂY

Đây là bài rất hay vì nhìn đề có vẻ phải mô phỏng rất nhiều cây, nhưng thực ra không cần mô phỏng.

Theo đề:

• Cây thứ 1 được đánh số 1
• Hai cây tiếp theo được đánh số 2
• Ba cây tiếp theo được đánh số 3
• Bốn cây tiếp theo được đánh số 4
• …

Tức là:

1. Viết thử ra giấy

Ta có:

Ví dụ:

Ta có:

Tổng số cây:

Chưa đến cây thứ 12.

Tiếp theo:

Các cây:

Do đó:

Đúng với ví dụ của đề.

2. Cách 1 — Mô phỏng đơn giản

Vì đề cho:

Ta không nên duyệt từ 1 đến N nếu muốn thuật toán tối ưu.

Nhưng để hiểu bài, có thể viết cách đơn giản:

N = int(input())

so = 1
tong = 0

while tong < N:
    tong += so
    if tong >= N:
        print(so)
        break

    so += 1

Ví dụ N = 12:

Vì:

nên đáp án là:

3. Độ phức tạp cách 1

Ta cần tìm k sao cho:

Mà:

nên:

Suy ra:

Vì vậy cách mô phỏng có độ phức tạp:

Với:

thì khoảng:

Chỉ khoảng vài chục nghìn vòng lặp → vẫn rất nhanh.

🟢 ĐÁP ÁN BÀI 3: TRÒ CHƠI VỚI BĂNG SỐ?

1. Đề bài

Trên một cuộn giấy dài, người ta lần lượt viết N số nguyên dương.

Yêu cầu: Cắt cuộn giấy thành nhiều đoạn nhất sao cho tổng các số trong mỗi đoạn bằng nhau.

Dữ liệu vào:

• Dòng đầu tiên chứa số nguyên dương N.
• Dòng thứ hai chứa N số nguyên dương a1, a2, ..., aN.

Dữ liệu ra:

• In ra số đoạn nhiều nhất có thể chia được.

Theo đề, N ≤ 10^3, vì vậy thuật toán O(N²) hoàn toàn phù hợp.

2. Hiểu đề bằng ví dụ

Ta có dãy:

10 2 6 2 5 2 1 2

Tổng tất cả các số là:

10 + 2 + 6 + 2 + 5 + 2 + 1 + 2 = 30

Có thể chia thành 3 đoạn:

Đoạn 1: 10
Đoạn 2: 2 + 6 + 2 = 10
Đoạn 3: 5 + 2 + 1 + 2 = 10

Như vậy:

10 | 2 6 2 | 5 2 1 2

Mỗi đoạn đều có tổng bằng 10.

Vì vậy kết quả là:

3

3. Nhận xét quan trọng

Gọi tổng toàn bộ dãy là:

S

Nếu chia được thành k đoạn bằng nhau thì tổng mỗi đoạn bắt buộc phải là:

S / k

Do đó:

S % k == 0

Nếu S không chia hết cho k thì chắc chắn không thể chia thành k đoạn có tổng bằng nhau.

Ví dụ:

S = 30

Ta có thể thử:

k = 8 → 30 không chia hết cho 8
k = 7 → 30 không chia hết cho 7
k = 6 → 30 chia hết cho 6
k = 5 → 30 chia hết cho 5
k = 3 → 30 chia hết cho 3
k = 2 → 30 chia hết cho 2
k = 1 → 30 chia hết cho 1

Nhưng mục tiêu là nhiều đoạn nhất, nên phải thử k từ lớn xuống nhỏ.

4. Tại sao thử số đoạn từ lớn xuống nhỏ?

Đề yêu cầu:

Chia thành nhiều đoạn nhất.

Giả sử có thể chia thành:

1 đoạn
2 đoạn
3 đoạn

thì đáp án phải là 3.

Vì vậy ta thử:

N, N-1, N-2, ..., 1

Ngay khi tìm được số đoạn hợp lệ đầu tiên thì đó chính là đáp án lớn nhất.

5. Cách kiểm tra một giá trị k

Giả sử:

S = 30
k = 3

Khi đó tổng mỗi đoạn phải là:

target = S // k
       = 30 // 3
       = 10

Ta duyệt dãy từ trái sang phải.

Ban đầu:

tong = 0

Đọc 10:

tong = 10

Đủ 10 nên tạo được đoạn thứ nhất:

10

Reset:

tong = 0

Đọc tiếp:

2
6
2

Ta có:

2 + 6 + 2 = 10

Tạo đoạn thứ hai.

Tiếp tục:

5 + 2 + 1 + 2 = 10

Tạo đoạn thứ ba.

Như vậy k = 3 hợp lệ.

6. Vì sao không được để tổng vượt target?

Giả sử:

target = 10

nhưng trong quá trình cộng ta có:

tong = 8

và phần tử tiếp theo là:

5

thì:

8 + 5 = 13 > 10

Đoạn hiện tại đã vượt quá 10.

Vì tất cả các số đều là số nguyên dương, ta không thể thêm hoặc bớt số nào để tổng quay lại bằng 10.

Do đó trường hợp này chắc chắn thất bại.

7. Thuật toán Bài 3

Các bước thực hiện:

Bước 1

Đọc N và dãy số.

Bước 2

Tính tổng toàn bộ dãy:

S = a1 + a2 + ... + aN

Bước 3

Thử số đoạn k từ N giảm xuống 1.

Bước 4

Nếu:

S % k != 0

thì bỏ qua k.

Bước 5

Tính:

target = S // k

Bước 6

Duyệt toàn bộ dãy.

Nếu:

tong + a[i] > target

thì k không hợp lệ.

Nếu:

tong + a[i] == target

thì hoàn thành một đoạn và đặt:

tong = 0

Bước 7

Nếu tạo được đúng k đoạn thì in k và kết thúc.

8. Code Python Bài 3

import sys

sys.stdin = open("BL3.INP", "r")
sys.stdout = open("BL3.OUT", "w")

n = int(input())
a = list(map(int, input().split()))

tong_all = sum(a)

# Thử số đoạn từ lớn xuống nhỏ
for k in range(n, 0, -1):

    # Tổng không chia hết cho k
    if tong_all % k != 0:
        continue

    target = tong_all // k

    # Nếu target nhỏ hơn phần tử lớn nhất
    # thì chắc chắn không thể chia
    if target < max(a):
        continue

    tong = 0
    dem = 0
    ok = True

    for x in a:

        tong += x

        # Tổng một đoạn đã vượt target
        if tong > target:
            ok = False
            break

        # Hoàn thành một đoạn
        if tong == target:
            dem += 1
            tong = 0

    # Kiểm tra có đúng k đoạn hay không
    if ok and tong == 0 and dem == k:
        print(k)
        break

9. Giải thích từng phần code Bài 3

Đọc dữ liệu

import sys

sys.stdin = open("BL3.INP", "r")
sys.stdout = open("BL3.OUT", "w")

Hai dòng:

sys.stdin = open("BL3.INP", "r")
sys.stdout = open("BL3.OUT", "w")

giúp chương trình đọc dữ liệu từ file BL3.INP và ghi kết quả vào BL3.OUT.

Đây là cách thường dùng trong các bài thi lập trình sử dụng file.

Đọc N và dãy số

n = int(input())
a = list(map(int, input().split()))

Ví dụ:

8
10 2 6 2 5 2 1 2

thì:

n = 8
a = [10, 2, 6, 2, 5, 2, 1, 2]

Tính tổng toàn bộ dãy

tong_all = sum(a)

Ta có:

tong_all = 30

Thử số đoạn từ lớn xuống

for k in range(n, 0, -1):

Nếu:

n = 8

thì:

k = 8
7
6
5
4
3
2
1

Mục đích là tìm số đoạn lớn nhất.

Kiểm tra tổng có chia hết cho k

if tong_all % k != 0:
    continue

Ví dụ:

30 % 7 != 0

nên không thể chia thành 7 đoạn bằng nhau.

Ta bỏ qua:

continue

Tính tổng mỗi đoạn

target = tong_all // k

Ví dụ:

30 / 3 = 10

Do đó mỗi đoạn phải có tổng bằng 10.

Biến tổng

tong = 0

Biến này lưu tổng của đoạn hiện tại.

Ví dụ đang xét:

2 6 2

thì:

tong = 2
tong = 8
tong = 10

Khi bằng target thì hoàn thành một đoạn.

Kiểm tra vượt quá target

if tong > target:
    ok = False
    break

Ví dụ:

target = 10
tong = 8
x = 5

thì:

tong = 13

vượt quá 10.

Do các số đều dương nên không thể sửa lại được.

Khi đủ một đoạn

if tong == target:
    dem += 1
    tong = 0

Ta tăng số đoạn:

dem += 1

sau đó bắt đầu đoạn mới:

tong = 0

10. Chạy thử Bài 3

Input:

8
10 2 6 2 5 2 1 2

Tổng:

30

Thử:

k = 8
30 không chia hết 8

k = 7
30 không chia hết 7

k = 6
target = 5

Phần tử đầu tiên là 10, lớn hơn 5 nên không thể.

Tiếp tục:

k = 5
target = 6

Phần tử đầu tiên 10 > 6, không thể.

Tiếp tục:

k = 3
target = 10

Ta chia được:

10
2 + 6 + 2 = 10
5 + 2 + 1 + 2 = 10

Vậy:

Đáp án = 3

Output:

3

11. Độ phức tạp Bài 3

Với mỗi giá trị k, ta có thể phải duyệt toàn bộ N phần tử.

Có tối đa N giá trị k cần thử.

Do đó độ phức tạp trong trường hợp xấu nhất là:

O(N²)

Bộ nhớ:

O(N)

do cần lưu dãy số.

Với N ≤ 1000 như đề bài, O(N²) tương đương khoảng tối đa một triệu phép kiểm tra, hoàn toàn phù hợp.

🟢GIẢI ĐÁP ÁN BÀI 4: XẾP HÀNG HÓA?

1. Đề bài

Tại một bến cảng, công nhân lần lượt bốc các kiện hàng từ tàu lên xe container.

Các kiện hàng phải được xử lý theo đúng thứ tự:

kiện 1 → kiện 2 → kiện 3 → ... → kiện n

Mỗi xe container có tải trọng tối đa là M.

Khi kiện hàng tiếp theo không thể đặt vào xe hiện tại vì tổng trọng lượng sẽ vượt quá M, phải chuyển sang xe tiếp theo.

Yêu cầu:

Tìm số chuyến xe ít nhất để vận chuyển hết hàng hóa.

Đây là bài toán tham lam – Greedy rất điển hình.

2. Ví dụ

Giả sử:

n = 10
M = 15

Các kiện hàng:

7 6 8 8 7 5 2 4 3 9

Ta xếp lần lượt.

Xe 1

7 + 6 = 13

Thêm 8:

13 + 8 = 21 > 15

Không được.

Xe 1:

7 + 6 = 13

Xe 2

Đặt:

8

Kiện tiếp theo 8:

8 + 8 = 16 > 15

Không được.

Xe 2:

8

Xe 3

Đặt:

8

Tiếp tục 7:

8 + 7 = 15

Vừa đủ.

Sau đó 5:

15 + 5 > 15

nên dừng.

Xe 3:

8 + 7 = 15

Tiếp tục tương tự:

Xe 4: 5 + 2 + 4 + 3 = 14
Xe 5: 9

Vậy cần:

5 chuyến xe

3. Ý tưởng Greedy

Điểm quan trọng nhất của bài này là:

Không được đổi thứ tự các kiện hàng.

Mỗi kiện hàng phải được đưa lên xe theo đúng thứ tự ban đầu.

Vì vậy ta chỉ cần quan tâm đến:

Xe hiện tại đang chở bao nhiêu?

Gọi:

tong

là tổng trọng lượng hàng đang nằm trên xe hiện tại.

Với mỗi kiện hàng x:

Trường hợp 1

Nếu:

tong + x <= M

thì kiện hàng vẫn đặt được lên xe hiện tại.

Ta thực hiện:

tong += x

Trường hợp 2

Nếu:

tong + x > M

thì kiện hàng không thể đặt lên xe hiện tại.

Bắt buộc phải sử dụng xe mới.

Ta:

so_xe += 1
tong = x

4. Tại sao cách Greedy là tối ưu?

Đây là phần rất quan trọng khi giải bài thi.

Giả sử xe hiện tại đang chứa tổng trọng lượng:

tong

và kiện tiếp theo có trọng lượng:

x

Nếu:

tong + x > M

thì xe hiện tại chắc chắn không thể chứa kiện x.

Không có cách nào khác để đưa x vào xe hiện tại, bởi vì:

• Không được bỏ kiện hàng trước đó.
• Không được đổi thứ tự.
• Không được đưa kiện x sang trước.
• Xe chỉ được chở tối đa M.

Do đó, bắt buộc phải mở xe mới.

Đây chính là lý do thuật toán tham lam hoạt động.

5. Thuật toán Bài 4

Bước 1

Đọc:

n, M

Bước 2

Đọc n trọng lượng.

Bước 3

Khởi tạo:

so_xe = 1
tong = 0

Vì n ≥ 1 nên ban đầu chắc chắn cần ít nhất một xe.

Bước 4

Duyệt từng kiện hàng x.

Nếu:

tong + x <= M

thì:

tong += x

Ngược lại:

so_xe += 1
tong = x

Bước 5

In:

so_xe

6. Code Python Bài 4

import sys

sys.stdin = open("BL4.INP", "r")
sys.stdout = open("BL4.OUT", "w")

n, M = map(int, input().split())
a = list(map(int, input().split()))

so_xe = 1
tong = 0

for x in a:

    if tong + x <= M:
        # Kiện hàng vẫn đặt được vào xe hiện tại
        tong += x
    else:
        # Không đủ chỗ, chuyển sang xe mới
        so_xe += 1
        tong = x

print(so_xe)

7. Giải thích code Bài 4

Đọc dữ liệu

n, M = map(int, input().split())

Ví dụ:

10 15

thì:

n = 10
M = 15

Trong đó:

• n: số kiện hàng.
• M: tải trọng tối đa của một xe.

Đọc trọng lượng

a = list(map(int, input().split()))

Ví dụ:

7 6 8 8 7 5 2 4 3 9

Khởi tạo

so_xe = 1
tong = 0

Ban đầu:

Chưa có hàng trên xe
Đang sử dụng xe số 1

Duyệt từng kiện

for x in a:

Mỗi vòng lặp lấy một kiện hàng.

Ví dụ:

x = 7

sau đó:

x = 6

rồi:

x = 8

Kiểm tra sức chứa

if tong + x <= M:

Nếu vẫn còn đủ tải trọng thì cho kiện hàng vào xe.

Ví dụ:

M = 15
tong = 7
x = 6

Ta có:

7 + 6 = 13 <= 15

nên:

tong += x

Kết quả:

tong = 13

Khi xe không chứa được kiện tiếp theo

Ví dụ:

tong = 13
x = 8
M = 15

Ta có:

13 + 8 = 21 > 15

Không thể đặt 8 vào xe hiện tại.

Ta mở xe mới:

so_xe += 1
tong = x

Kết quả:

so_xe = 2
tong = 8

8. Chạy thử Bài 4

Input:

10 15
7 6 8 8 7 5 2 4 3 9

Quá trình:

Xe 1:
7 + 6 = 13

Xe 2:
8

Xe 3:
8 + 7 = 15

Xe 4:
5 + 2 + 4 + 3 = 14

Xe 5:
9

Kết quả:

5

Output:

5

Ví dụ này cũng trùng với ví dụ được đăng lại từ đề bài.

9. Độ phức tạp Bài 4

Ta chỉ duyệt qua dãy đúng một lần.

Nếu có N kiện hàng:

Thời gian: O(N)

Bộ nhớ ngoài mảng đầu vào:

O(1)

Nếu lưu toàn bộ dãy:

O(N)

Có thể viết chương trình tiết kiệm bộ nhớ hơn bằng cách đọc từng số, nhưng với đề thi thông thường thì lưu mảng như trên rất dễ hiểu.

10. So sánh hai bài toán

11. Những lỗi thường gặp

Lỗi 1: Bài 3 chỉ tìm một cách chia

Đề yêu cầu:

nhiều đoạn nhất

Do đó không được dừng ở cách chia đầu tiên tìm thấy nếu đang thử số đoạn từ nhỏ lên.

Cách tốt hơn là:

N → N-1 → N-2 → ... → 1

Lỗi 2: Quên kiểm tra tổng chia hết

Ví dụ:

S = 30
k = 7

Không thể có tổng mỗi đoạn là:

30 / 7

vì không phải số nguyên.

Do đó cần:

if tong_all % k != 0:
    continue

Lỗi 3: Bài 3 cho phép tổng vượt target

Không được.

Nếu:

target = 10
tong = 8
x = 5

thì:

tong = 13

Đoạn đó thất bại ngay.

Lỗi 4: Bài 4 sắp xếp các kiện hàng

Không được viết:

a.sort()

Bởi vì đề yêu cầu các kiện hàng phải được bốc lần lượt theo thứ tự ban đầu.

Ví dụ:

7 6 8 8 7

không được biến thành:

6 7 7 8 8

Lỗi 5: Dùng bài toán ba lô hoặc tìm mọi cách kết hợp

Bài 4 không yêu cầu tìm cách sắp xếp tối ưu tùy ý.

Thứ tự kiện hàng đã cố định.

Vì vậy chỉ cần:

nhét được → nhét
không nhét được → xe mới

Đây là tư duy Greedy.

12. Mẹo ghi nhớ nhanh

Bài 3

Hãy nhớ 4 bước:

TỔNG → THỬ k → TÍNH TARGET → KIỂM TRA

Trong đó:

target = Tổng / k

và thử:

k từ lớn xuống nhỏ

Bài 4

Chỉ cần nhớ:

Còn chỗ → cho vào
Hết chỗ → xe mới

Công thức kiểm tra:

tong + x <= M

Nếu đúng:

tong += x

Nếu sai:

so_xe += 1
tong = x

13. Phiên bản code ngắn gọn Bài 3

Sau khi đã hiểu thuật toán, có thể viết ngắn hơn:

import sys

sys.stdin = open("BL3.INP", "r")
sys.stdout = open("BL3.OUT", "w")

n = int(input())
a = list(map(int, input().split()))

S = sum(a)

for k in range(n, 0, -1):
    if S % k != 0:
        continue

    target = S // k
    tong = 0
    dem = 0

    for x in a:
        tong += x

        if tong > target:
            break

        if tong == target:
            dem += 1
            tong = 0

    if dem == k and tong == 0:
        print(k)
        break

14. Phiên bản code ngắn gọn Bài 4

import sys

sys.stdin = open("BL4.INP", "r")
sys.stdout = open("BL4.OUT", "w")

n, M = map(int, input().split())
a = list(map(int, input().split()))

xe = 1
tong = 0

for x in a:
    if tong + x <= M:
        tong += x
    else:
        xe += 1
        tong = x

print(xe)

15. Kết luận

Hai bài toán nhìn qua khá giống nhau vì đều yêu cầu chia một dãy số thành các nhóm liên tiếp, nhưng cách tư duy hoàn toàn khác nhau.

Bài 3 – Trò chơi với băng số:

• Tính tổng toàn bộ dãy.
• Muốn chia thành k đoạn thì tổng mỗi đoạn phải là S/k.
• Thử k từ lớn xuống nhỏ.
• Dùng tổng tích lũy để kiểm tra.
• Với N ≤ 1000, thuật toán O(N²) là phù hợp.

Bài 4 – Xếp hàng hóa:

• Không được thay đổi thứ tự kiện hàng.
• Duyệt từ trái sang phải.
• Nếu kiện tiếp theo vẫn vừa xe thì cho vào.
• Nếu không vừa thì mở xe mới.
• Thuật toán Greedy có độ phức tạp O(N).

Đây là hai dạng bài rất đáng học vì giúp hình thành hai kỹ thuật quan trọng trong lập trình thi đấu:

Bài 3 → Duyệt các khả năng + kiểm tra tổng
Bài 4 → Thuật toán tham lam (Greedy)

Nếu nắm chắc hai mẫu tư duy này, bạn sẽ gặp rất nhiều bài tương tự trong các đề thi học sinh giỏi Tin học.

Tại Sao Bạn Nên Luyện Đề Thi Này?

• Bám sát thực tế: Đề thi phản ánh đúng độ khó và xu hướng ra đề của các huyện trong khu vực.

• Rèn tư duy tối ưu: Giúp học sinh chuyển dịch từ tư duy “viết code cho chạy được” sang “viết code tối ưu thời gian $O(N)$ và bộ nhớ”.

• Đa dạng ngôn ngữ: Đề bài hỗ trợ giải bằng cả Python, Pascal, hoặc C++.

Tải Xuống Trọn Bộ Đề Thi & Đáp Án Chi Tiết

Bộ file tải về bao gồm:

1. File đề thi gốc định dạng PDF (sắc nét, dễ in ấn).

2. Đáp án chi tiết và hướng dẫn chấm điểm.

3. Bộ Test mẫu (Input/Output) và Code mẫu (C++ / Python) đã qua kiểm thử thành công.

👉 LINK TẢI VỀ TRỌN BỘ ĐỀ THI & CODE MẪU (GOOGLE DRIVE) (Nhấp vào để tải miễn phí)

Bí Quyết Ôn Luyện HSG Tin Học Đạt Giải Cao

• Nắm chắc nền tảng: Ôn tập kỹ kiến thức mảng, chuỗi, các hàm toán học và câu lệnh lặp.

• Tối ưu thời gian chạy: Luôn chú ý đến giới hạn $N$ của đề bài để chọn thuật toán phù hợp, tránh lỗi TLE (Time Limit Exceeded).

• Luyện tập thường xuyên: Làm lại đề thi các năm trước và tham gia giải bài trên các hệ thống chấm công khai (Online Judge).

 Vi Tính Tấn Dân – Đồng Hành Cùng Tri Thức & Công Nghệ

Bên cạnh việc chia sẻ kiến thức và tài liệu học tập miễn phí, Vi Tính Tấn Dân tự hào là đơn vị uy tín chuyên cung cấp:

•  Dàn máy tính PC Lập trình – Học tập – Chơi game cấu hình tối ưu, giá rẻ.

•  Dịch vụ sửa chữa, nâng cấp Laptop & PC nhanh chóng, tận tâm tại Đồng Tháp.

•  Linh phụ kiện máy tính chính hãng (Bàn phím, chuột, màn hình, SSD…).

Nếu bạn đang tìm kiếm một chiếc máy tính mượt mà để phục vụ việc học lập trình C++, Python hay Pascal, hãy liên hệ ngay với Vi Tính Tấn Dân để nhận được sự tư vấn chu đáo nhất!

7. Cách thức đăng ký và đóng học phí như thế nào?

Bạn có thể liên hệ trực tiếp với Thầy qua các kênh sau để được tư vấn và nhận báo giá ưu đãi:

• Số điện thoại / Zalo: 0937.179.278

• Hình thức đóng phí: Chuyển khoản ngân hàng hoặc nộp trực tiếp tại cơ sở (nếu học offline).

Nếu bạn thấy hay ! xin bạn 1 phút ! vui lòng đánh giá 5 sao cho trang website của chúng tôi ! để có động lực làm thêm nhiều bài hay nữa ! cảm ơn quý khách nhé !

 Thông Tin Liên Hệ:

• Website: vitinhtandan.com

• Hotline/Zalo: (0937.179.278)

• Địa chỉ: (Tổ 5, Ấp Tân Lược 1, xã Tân Hương, Đồng Tháp)

Chúc các bạn học sinh ôn luyện thật tốt và đạt kết quả cao nhất trong kỳ thi Học sinh giỏi Tin học lớp 9 sắp tới!

#HSGTinHoc #DeThiHSGTinHoc #TinHocTHCS #TanPhuoc #LapTrinhPython #LapTrinhCPP #HocSinhGioiTinHoc #OnThiHSG #KhungThuatToan #ViTinhTanDan #TinHocTanDan

Kỳ thi Học sinh giỏi (HSG) Tin học lớp 9 cấp xã và tỉnh luôn là một trong những thử thách lớn đối với các bạn học sinh đam mê lập trình và thuật toán. Để đạt được thành tích cao, việc luyện đề và cọ xát với các dạng bài thi thực tế từ các năm trước là phương pháp ôn luyện vô cùng hiệu quả.

Nhằm đồng hành cùng các bạn học sinh và quý thầy cô trên địa bàn tỉnh, Vi Tính Tấn Dân xin chia sẻ Bộ 21 Đề thi HSG Tin học lớp 9 Đồng Tháp năm học 2026 – 2027 (Kèm đáp án và hướng dẫn giải chi tiết).

📌 Tổng Quan Tệp Tài Liệu Đề Thi HSG Tin Học Lớp 9 Đồng Tháp

Bộ tài liệu được sưu tầm, tuyển chọn và biên soạn kỹ lưỡng, bám sát cấu trúc đề thi chính thức của Sở GD&ĐT Tỉnh Đồng Tháp qua các kỳ thi gần đây.

Bộ 21 Đề Thi HSG Tin Học Lớp 9 Đồng Tháp 2026 – 2027 (Có Đáp Án)

• Các đề ôn thi để chuẩn bị thi Cấp Huyện thì các em vào đường dẫn phía dưới để tham khảo giúp thầy nhé!
  1. Giải đề 1 và đáp án thi Học sinh giỏi tin học Python C++ THCS có tài liệu ôn thi
  2. Giải đề 2 và đáp án thi Học sinh giỏi tin học Python C++ THCS có tài liệu ôn thi
  3. Giải đề 3 thi học sinh giỏi tin học lập trình Python có đáp án
  4. Giải đề 4 ôn thi học sinh giỏi Tin Học THCS lập trình Python có đáp án
  5. Giải đề 5 và đáp án thi HSG Tin Python có số Pell.
  6. Giải đề 6 và đáp án bồi dưỡng học sinh giỏi tin 10 có số Armstrong
  7. Giải đề 7 và đáp án  thi học sinh giỏi tin học 10 Python có số Collatz
  8. Giải đề 8 trong 20 đề Bồi dưỡng học sinh giỏi Tin học lớp 9 có số Kaprekar.
  9. Giải đề 9 thi HSG Tin học lớp 8 lập trình Python có số Happy
  10. Giải đề 10 thi tin học trẻ THPT có bài  In các xâu con trong xâu s.
  11. Đề thi hsg tin 11 python có đáp án hay nhất 2024
  12. 12 đề và đáp án thi HSG tin Python có sắp xếp
  13. Đề 13 thi học sinh giỏi Tin học THCS có đáp án hay nhất năm 2024.
  14. 14 đề bồi dưỡng học sinh giỏi tin học lớp 7, 8, 9 THCS mới nhất !
  15. 15 Đề thi học sinh giỏi Tin học lớp 9 cấp huyện hay nhất 2024 – 2025
  16. 16 Đề bài tập Python có lời giải PDF thi HSG cấp huyện mới nhất
  17. 17 đề thi tin học trẻ có Đáp Án python THCS cấp huyện PDF
  18. 18 Đề thi học sinh giỏi Tin học THCS có đáp ÁN dễ học nhất năm 2025
  19. 19 thi HSG Tin 9 C ++ hoặc Python có đáp án
  20. 100 đề và đáp án thi HSG tin Python cấp huyện 2025
  21. Bộ 21 Đề thi HSG Tin học lớp 9 Đồng Tháp năm học 2026 – 2027 (Kèm đáp án )

Bộ 21 Đề Thi HSG Tin Học Lớp 9 Đồng Tháp 2026 – 2027 (Có Đáp Án)

Đáp án đề thi HSG Tin học lớp 9 cấp thị xã Gò Công:

Đây là một đề HSG THCS khá hay, gồm 5 bài với mức độ từ cơ bản → vận dụng. Mình sẽ phân tích từng bài theo đúng phong cách luyện HSG:

• Ý tưởng
• Thuật toán
• Độ phức tạp
• Lưu ý dễ sai
• Code Python dùng sys.stdin=open(...)
• Giải thích từng dòng

Đáp Án Bài 1: DAY – Ngày lắng nghe:

Đề bài

Cho một ngày dạng

dd/mm

14/02

BEFORE

AFTER

EXACTLY

Phân tích

Ví dụ

15/01

thì

15/1 < 14/2

Ví dụ

01/03

lớn hơn tháng 2

=> AFTER

Ý tưởng

Có hai trường hợp

Nếu tháng nhỏ hơn 2

BEFORE

AFTER

So tiếp ngày.

day<14

day==14

day>14

Thuật toán

Đọc chuỗi
Tách ngày và tháng
Nếu month<2
      BEFORE
Nếu month>2
      AFTER
Nếu month==2
      day<14
            BEFORE
      day==14
            EXACTLY
      day>14
            AFTER

Độ phức tạp

Đọc đúng 1 lần

O(1)

O(1)

Code Python

import sys
sys.stdin = open("DAY.INP", "r")
sys.stdout = open("DAY.OUT", "w")
s = input()
ngay, thang = map(int, s.split("/"))
if thang < 2:
    print("BEFORE")
elif thang > 2:
    print("AFTER")
else:
    if ngay < 14:
        print("BEFORE")
    elif ngay == 14:
        print("EXACTLY")
    else:
        print("AFTER")

Chú ý

Nhiều bạn so sánh

dd/mm

Ví dụ

9/2
14/2

Phải chuyển sang số nguyên.

Đáp Án Bài 2: SUNFLOWER

Đề

Có n bông hoa.

Hoa đặc biệt nếu số hạt là số nguyên tố.

Đếm có bao nhiêu hoa đặc biệt.

1≤n≤10000

ai≤10^12

Phân tích

Ví dụ

1 4 3

3

Đáp án

1

Khó ở đâu?

ai≤10^12

Ta phải kiểm tra nguyên tố từng số.

Kiểm tra nguyên tố

Một số nguyên tố chỉ cần thử đến

√n

97

chỉ thử

2
3
5
7

Thuật toán kiểm tra

Nếu

n<2

Nếu

2

Nếu

chia hết cho 2

Sau đó

3
5
7
9
11
...

2

√n

không nguyên tố.

Ngược lại

nguyên tố.

Vì sao đúng?

Nếu

n=a×b

a≤√n

Thuật toán

ans=0
lặp qua từng ai
      nếu nguyên tố
             ans+=1
in ans

Độ phức tạp

Giả sử

M=max(ai)

O(√M)

√10^12=10^6

O(n√M)

• gặp ước sẽ dừng sớm
• nhiều số chẵn
• n chỉ 10000

Code Python

import sys
import math

sys.stdin = open("SUNFLOWER.INP", "r")
sys.stdout = open("SUNFLOWER.OUT", "w")


def nguyen_to(x):
    if x < 2:
        return False

    if x == 2:
        return True

    if x % 2 == 0:
        return False

    i = 3

    while i <= math.isqrt(x):
        if x % i == 0:
            return False
        i += 2

    return True


n = int(input())

a = list(map(int, input().split()))

dem = 0

for x in a:
    if nguyen_to(x):
        dem += 1

print(dem)

Vì sao dùng math.isqrt()

Thay vì

int(math.sqrt(x))

math.isqrt(x)

• Chính xác với số rất lớn.
• Không bị sai số số thực.
• Nhanh hơn.

Các lỗi thường gặp

Sai 1

1

Sai 2

Quên xét

2

Sai 3

Thử đến

n

√n

Sai 4

Dùng

for i in range(2, x):

10^12

Tổng kết

Đáp Án Bài 3: ROBOT (4 điểm)

Đề bài

Có

• n cây
• vị trí robot là p
• pin đủ đi được k đơn vị chỉ từ trái sang phải

Có n cây tại các vị trí

a1 < a2 < ... < an

Ví dụ

4 3 4

2 5 6 9

ở vị trí

3

4

nên tới

7

[3 ; 7]

5
6

2

Phân tích

Robot KHÔNG quay lại.

Robot chỉ đi

p → p+k

p ≤ ai ≤ p+k

Đếm bao nhiêu số nằm trong đoạn [L,R].

Ý tưởng 1 (dễ hiểu)

Duyệt toàn bộ mảng.

Nếu

p<=ai<=p+k

dem+=1

Thuật toán

Đọc dữ liệu

dem=0

For mỗi cây

    nếu p<=ai<=p+k

          dem++

In dem

Độ phức tạp

Có

n≤10^6

Chỉ duyệt đúng một lần.

Thời gian

O(n)

Bộ nhớ

O(n)

(vì lưu mảng)

Nếu đọc từng số cũng chỉ O(1) bộ nhớ.

Vì sao đúng?

Mỗi cây chỉ có hai khả năng

• nằm trong đoạn
• không nằm trong đoạn

Duyệt hết một lần sẽ không bỏ sót.

Code Python

import sys
sys.stdin = open("ROBOT.INP", "r")
sys.stdout = open("ROBOT.OUT", "w")
n, p, k = map(int, input().split())
a = list(map(int, input().split()))
dem = 0
for x in a:
    if p <= x <= p + k:
        dem += 1
print(dem)

Nếu muốn nhanh hơn?

Do dãy đã tăng dần

Có thể dùng

binary search

tìm

• vị trí đầu tiên ≥ p
• vị trí cuối cùng ≤ p+k

Độ phức tạp

O(log n)

nhưng đề này O(n) đã đủ.

Các lỗi thường gặp

Sai

if x>p and x<p+k

Sẽ bỏ mất cây ở

p

hoặc

p+k

Phải là

if p<=x<=p+k

Đáp Án Bài 4: LAVENDER

Đề

Có

m dòng

n cột

Ma trận

Đếm số phần tử

>=T

Ví dụ

2 3 50

10 12 50

44 60 55

Có

50

60

55

=>3

Phân tích

Không yêu cầu tìm vị trí.

Không yêu cầu sắp xếp.

Chỉ cần đếm.

Ý tưởng

Đọc từng số

Nếu

>=T

thì tăng biến đếm.

Thuật toán

Đọc
m n T
dem=0
Lặp m lần
      đọc một dòng
      duyệt n số
            nếu >=T
                  dem++
In dem

Độ phức tạp

Có

m,n≤1000

10^6

Thời gian

O(mn)

O(n)

Vì sao đúng?

Mỗi phần tử được xét đúng một lần.

Không bỏ sót.

Code

import sys

sys.stdin = open("LAVENDER.INP", "r")
sys.stdout = open("LAVENDER.OUT", "w")

m, n, T = map(int, input().split())

dem = 0

for _ in range(m):

    dong = list(map(int, input().split()))

    for x in dong:

        if x >= T:
            dem += 1

print(dem)

Tối ưu bộ nhớ

Không cần

a=[]

Đọc từng dòng là tốt nhất.

Lỗi thường gặp

Viết

if x>T

Đề là

>=T

Đáp Án Bài 5: ESSENCE

Đề

Cho chuỗi

Ví dụ

ABCCDZDC

Độ đậm đặc

=

số lần xuất hiện nhiều nhất của một ký tự.

Ví dụ

A :1

B :1

C :3

D :2

Z :1

Đáp án

3

Phân tích

Đây chính là

tần số lớn nhất.

Cách 1 (đơn giản)

Dùng Dictionary.

Ý tưởng

Duyệt chuỗi.

Nếu ký tự chưa có

thêm vào.

Nếu có

tăng lên 1.

Sau đó lấy giá trị lớn nhất.

Thuật toán

Đọc chuỗi

Dictionary rỗng

For ký tự

      tăng số lần xuất hiện

In max(dictionary.values())

Độ phức tạp

Chuỗi dài

1000

O(n)

O(26)

Vì sao đúng?

Dictionary lưu đúng số lần xuất hiện từng ký tự.

Giá trị lớn nhất chính là đáp án.

Code Python

import sys

sys.stdin = open("ESSENCE.INP", "r")
sys.stdout = open("ESSENCE.OUT", "w")

s = input()

dem = {}

for ch in s:

    if ch not in dem:
        dem[ch] = 1
    else:
        dem[ch] += 1

print(max(dem.values()))

Cách 2 (đẹp hơn)

Dùng mảng 26 phần tử.

Ý tưởng

A ->0

B ->1

...

Z ->25

Mỗi lần gặp

ord(ch)-ord('A')

Code Python

import sys

sys.stdin = open("ESSENCE.INP", "r")
sys.stdout = open("ESSENCE.OUT", "w")

s = input()

cnt = [0] * 26

for ch in s:

    cnt[ord(ch) - ord('A')] += 1

print(max(cnt))

Vì sao mảng nhanh hơn Dictionary?

• Truy cập trực tiếp theo chỉ số (O(1) với hằng số rất nhỏ).
• Không cần băm (hash).
• Chỉ có 26 chữ cái nên rất phù hợp.

Tổng kết cả đề

🎯 Nhận xét về Cấu Trúc Trọng Tâm Trong Đề Thi HSG Tin Học 9 Đồng Tháp

Đây là đề HSG THCS thiên về kỹ năng lập trình cơ bản, chưa yêu cầu các thuật toán nâng cao như quy hoạch động, đồ thị hay cây dữ liệu.

Các kiến thức chính được kiểm tra gồm:

• Bài 1: Rẽ nhánh (if...elif...else).
• Bài 2: Hàm kiểm tra số nguyên tố và tối ưu đến √n.
• Bài 3: Duyệt mảng, xử lý đoạn giá trị; có thể mở rộng bằng tìm kiếm nhị phân.
• Bài 4: Duyệt ma trận và đếm theo điều kiện.
• Bài 5: Đếm tần suất bằng dict hoặc mảng đếm.

Đây là một đề rất phù hợp để ôn luyện cho học sinh mới bắt đầu thi HSG Tin học vì bao quát nhiều kỹ năng nền tảng quan trọng.

💡 Lời khuyên từ Vi Tính Tấn Dân: Đề thi Tin học lớp 9 hiện nay hướng nhiều đến tư duy thuật toán tối ưu thời gian (O(N \logN) hoặc O(N)). Luyện tập thường xuyên với bộ đề này sẽ giúp bạn làm quen với áp lực thời gian và hạn chế tối đa các lỗi quá thời gian (Time Limit Exceeded).

73 Đề thi HSG Tin học Python THCS cấp tỉnh Tiền Giang có ĐÁP ÁN (Mới & Chọn Lọc)

📥 Link Tải Bộ 21 Đề Thi HSG Tin Học 9 Đồng Tháp (File Chuẩn)

Các bạn học sinh và thầy cô có thể tải trọn bộ đề thi hoàn toàn miễn phí theo đường dẫn dưới đây:

👉 [LINK TẢI TRỌN BỘ 21 ĐỀ THI HSG TIN HỌC LỚP 9 ĐỒNG THÁP (PDF/WORD)]

(Lưu ý: Nếu gặp bất kỳ lỗi nào trong quá trình tải file, vui lòng để lại bình luận bên dưới để Vi Tính Tấn Dân hỗ trợ kịp thời!)

🖥️ Vi Tính Tấn Dân – Đồng Hành Cùng Tri Thức & Công Nghệ

Bên cạnh việc chia sẻ kiến thức và tài liệu học tập miễn phí, Vi Tính Tấn Dân tự hào là đơn vị uy tín chuyên cung cấp:

• 💻 Dàn máy tính PC Lập trình – Học tập – Chơi game cấu hình tối ưu, giá rẻ.

• 🛠️ Dịch vụ sửa chữa, nâng cấp Laptop & PC nhanh chóng, tận tâm tại Đồng Tháp.

• 🎧 Linh phụ kiện máy tính chính hãng (Bàn phím, chuột, màn hình, SSD…).

Nếu bạn đang tìm kiếm một chiếc máy tính mượt mà để phục vụ việc học lập trình C++, Python hay Pascal, hãy liên hệ ngay với Vi Tính Tấn Dân để nhận được sự tư vấn chu đáo nhất!

7. Cách thức đăng ký và đóng học phí như thế nào?

Bạn có thể liên hệ trực tiếp với Thầy qua các kênh sau để được tư vấn và nhận báo giá ưu đãi:

• Số điện thoại / Zalo: 0937.179.278

• Hình thức đóng phí: Chuyển khoản ngân hàng hoặc nộp trực tiếp tại cơ sở (nếu học offline).

Nếu bạn thấy hay ! xin bạn 1 phút ! vui lòng đánh giá 5 sao cho trang website của chúng tôi ! để có động lực làm thêm nhiều bài hay nữa ! cảm ơn quý khách nhé !

📞 Thông Tin Liên Hệ:

• Website: vitinhtandan.com

• Hotline/Zalo: (0937.179.278)

• Địa chỉ: (Tổ 5, Ấp Tân Lược 1, xã Tân Hương, Đồng Tháp)

Chúc các bạn học sinh ôn luyện thật tốt và đạt kết quả cao nhất trong kỳ thi Học sinh giỏi Tin học lớp 9 sắp tới!

Dưới đây là phần Câu Hỏi Thường Gặp (FAQ) chuẩn SEO dành riêng cho bài viết. Đoạn này không chỉ giúp giữ chân người đọc lâu hơn mà còn rất dễ được Google đưa lên vị trí Featured Snippet (Top 0) hoặc hiển thị trong mục “Mọi người cũng hỏi”:

❓ Câu Hỏi Thường Gặp (FAQ) – Đề Thi HSG Tin Học 9 Đồng Tháp

1. Bộ đề thi HSG Tin học lớp 9 Đồng Tháp có đáp án chi tiết không?

Trả lời: Có. Bộ 21 đề thi HSG Tin học 9 Đồng Tháp do Vi Tính Tấn Dân tổng hợp đều đi kèm đáp án, hướng dẫn giải chi tiết, test case mẫu và code tham khảo bằng các ngôn ngữ phổ biến như C++, Python và Pascal.

2. Tải bộ đề thi HSG Tin học 9 Đồng Tháp 2026 – 2027 có mất phí không?

Trả lời: Hoàn toàn MIỄN PHÍ. Bạn chỉ cần bấm vào đường link Google Drive được đính kèm trong bài viết là có thể tải toàn bộ file PDF/Word về máy để in ấn và học tập dễ dàng.

3. Đề thi HSG Tin học lớp 9 Đồng Tháp thường sử dụng ngôn ngữ lập trình nào?

Trả lời: Hiện nay, các kỳ thi Học sinh giỏi Tin học THCS tại Đồng Tháp ưu tiên sử dụng ngôn ngữ C++ và Python nhờ tối ưu tốc độ và thư viện phong phú. Tuy nhiên, một số bài thi vẫn chấp nhận Pascal. Học sinh nên tập trung luyện tập kĩ năng tư duy thuật toán trên C++ hoặc Python để đạt điểm tối đa.

4. Học sinh lớp 9 cần tập trung những dạng thuật toán nào để thi HSG Tin học?

Trả lời: Cấu trúc đề thi HSG Tin học 9 Đồng Tháp thường xoay quanh các dạng bài trọng tâm:

• Xử lý chuỗi, mã hóa và số học cơ bản.

• Thuật toán tìm kiếm nhị phân, kỹ thuật hai con trỏ, mảng cộng dồn.

• Sắp xếp tối ưu $O(N \log N)$.

• Quy hoạch động cơ bản (Đếm cách, Tối ưu hóa).

5. Học lập trình nên chọn cấu hình máy tính/laptop như thế nào?

Trả lời: Để phục vụ tốt việc học lập trình C++, Python và chạy các phần mềm như Code::Blocks, VS Code, PyCharm…, bạn nên chọn PC/Laptop có cấu hình tối thiểu:

• CPU: Core i3/Ryzen 3 trở lên (thế hệ mới).

• RAM: Tối thiểu 8GB.

• Ổ cứng: SSD 256GB để khởi động phần mềm mượt mà.

📌 Nếu bạn cần tư vấn chọn máy tính học tập – lập trình phù hợp với ngân sách, hãy liên hệ ngay hotline của Vi Tính Tấn Dân để được hỗ trợ tốt nhất!

6 BÀI TẬP C++ CHUẨN THI HỌC SINH GIỎI MỚI NHẤT 2026

Tài liệu này tổng hợp các bài toán lập trình C++ từ căn bản đến nâng cao được thiết kế hoàn toàn theo format các kỳ thi Học sinh giỏi (HSG) các cấp. Mỗi bài toán đều quy định rõ ràng tệp dữ liệu vào, tệp kết quả ra, giới hạn dữ liệu (subtasks) và kèm theo mã nguồn giải mẫu tối ưu, sử dụng định danh biến bằng tiếng Việt trực quan, giúp học sinh nắm vững bản chất thuật toán.

Bài 1: Tính toán kích thước hình học (HCN)

Bài toán: Cho hai số thực dương là chiều dài và chiều rộng của một mảnh vườn hình chữ nhật. Tính chu vi và diện tích mảnh vườn. Kết quả làm tròn đến 2 chữ số thập phân.

• Thời gian chạy: 1.0 giây

• Dữ liệu vào (HCN.INP): Một dòng chứa hai số thực $a$ và $b$ (0 < a, b ≤ 10^6).

• Dữ liệu ra (HCN.OUT): Một dòng chứa chu vi và diện tích, cách nhau một khoảng trắng.

Ví dụ:

• Input (HCN.INP): 5.5 3.2

• Output (HCN.OUT): 17.40 17.60

Code C++ tham khảo:

#include <iostream>
#include <iomanip>
using namespace std;

int main() {
    freopen("HCN.INP", "r", stdin);
    freopen("HCN.OUT", "w", stdout);

    double dai, rong;
    if (cin >> dai >> rong) {
        double chu_vi = (dai + rong) * 2;
        double dien_tich = dai * rong;
        cout << fixed << setprecision(2) << chu_vi << " " << dien_tich << endl;
    }
    return 0;
}

Bài 2: Khảo sát số nguyên tố lớn (SNT)

Bài toán: Kiểm tra số nguyên dương $N$ có phải là số nguyên tố hay không.

• Thời gian chạy: 1.0 giây

• Dữ liệu vào (SNT.INP): Số nguyên dương $N$.

  • Subtask 1 (60%): N ≤ 10^6

  • Subtask 2 (40%): N ≤ 10^12

• Dữ liệu ra (SNT.OUT): In ra YES nếu là số nguyên tố, ngược lại in NO.

Ví dụ:

• Input (SNT.INP): 97

• Output (SNT.OUT): YES

Code C++ tham khảo:

#include <iostream>
#include <cmath>
using namespace std;

int main() {
    freopen("SNT.INP", "r", stdin);
    freopen("SNT.OUT", "w", stdout);

    long long n; 
    cin >> n;

    if (n < 2) {
        cout << "NO\n";
        return 0;
    }

    bool la_snt = true;
    long long can_bac_hai = sqrt(n);
    
    for (long long i = 2; i <= can_bac_hai; i++) {
        if (n % i == 0) {
            la_snt = false;
            break;
        }
    }

    if (la_snt) cout << "YES\n";
    else cout << "NO\n";
    
    return 0;
}

Bài 3: Thống kê ký tự nguyên âm (CHUOI)

Bài toán: Đếm số lượng nguyên âm (‘a’, ‘e’, ‘i’, ‘o’, ‘u’) trong một chuỗi ký tự.

• Thời gian chạy: 1.0 giây

• Dữ liệu vào (CHUOI.INP): Chuỗi ký tự $S$ (chiều dài ≤ 1000).

• Dữ liệu ra (CHUOI.OUT): Số lượng nguyên âm đếm được.

Ví dụ:

• Input (CHUOI.INP): Lap trinh C++ Chuan HSG

• Output (CHUOI.OUT): 5

Code C++ tham khảo:

#include <iostream>
#include <string>
using namespace std;

int main() {
    freopen("CHUOI.INP", "r", stdin);
    freopen("CHUOI.OUT", "w", stdout);

    string van_ban;
    getline(cin, van_ban); 

    int bien_dem = 0;
    for (int i = 0; i < van_ban.length(); i++) {
        char ky_tu = tolower(van_ban[i]);
        if (ky_tu == 'a' || ky_tu == 'e' || ky_tu == 'i' || ky_tu == 'o' || ky_tu == 'u') {
            bien_dem++;
        }
    }

    cout << bien_dem << endl;
    return 0;
}

Bài 4: Sắp xếp và tối ưu mảng số (SAPXEP)

Bài toán: Sắp xếp mảng $N$ số nguyên theo thứ tự tăng dần.

• Thời gian chạy: 1.0 giây

• Dữ liệu vào (SAPXEP.INP): * Dòng 1: Số nguyên $N$ (N ≤ 10^5).

  • Dòng 2: $N$ số nguyên cách nhau một dấu cách.

• Dữ liệu ra (SAPXEP.OUT): Mảng đã sắp xếp tăng dần.

Ví dụ:

• Input (SAPXEP.INP):

  5

  12 -3 7 0 5

• Output (SAPXEP.OUT): -3 0 5 7 12

Code C++ tham khảo:

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

int main() {
    freopen("SAPXEP.INP", "r", stdin);
    freopen("SAPXEP.OUT", "w", stdout);

    int so_luong;
    if (cin >> so_luong) {
        vector<int> danh_sach(so_luong);
        
        for (int i = 0; i < so_luong; i++) {
            cin >> danh_sach[i];
        }

        sort(danh_sach.begin(), danh_sach.end());

        for (int i = 0; i < so_luong; i++) {
            cout << danh_sach[i] << " ";
        }
        cout << endl;
    }
    return 0;
}

Bài 5: Tối giản phân số bằng OOP (PHANSO)

Bài toán: Dùng lập trình hướng đối tượng xây dựng lớp Phân số để cộng 2 phân số và in ra kết quả tối giản.

• Thời gian chạy: 1.0 giây

• Dữ liệu vào (PHANSO.INP): 4 số nguyên: Tử 1, Mẫu 1, Tử 2, Mẫu 2 (trong khoảng -10^4 đến 10^4).

• Dữ liệu ra (PHANSO.OUT): Phân số tổng tối giản (nếu mẫu là 1 chỉ in tử số).

Ví dụ:

• Input (PHANSO.INP): 1 6 2 3

• Output (PHANSO.OUT): 5/6

Code C++ tham khảo:

#include <iostream>
#include <cmath>
using namespace std;

class PhanSo {
private:
    long long tu, mau;

    long long tim_ucln(long long a, long long b) {
        a = abs(a); b = abs(b);
        while (b != 0) {
            long long tam = b;
            b = a % b;
            a = tam;
        }
        return a;
    }

public:
    PhanSo(long long t = 0, long long m = 1) {
        tu = t;
        mau = (m == 0) ? 1 : m;
    }

    void toi_gian() {
        long long ucln = tim_ucln(tu, mau);
        tu /= ucln;
        mau /= ucln;
        if (mau < 0) { 
            tu = -tu;
            mau = -mau;
        }
    }

    PhanSo cong(PhanSo doi_tac) {
        PhanSo ket_qua;
        ket_qua.tu = this->tu * doi_tac.mau + doi_tac.tu * this->mau;
        ket_qua.mau = this->mau * doi_tac.mau;
        ket_qua.toi_gian();
        return ket_qua;
    }

    void in_ket_qua() {
        if (mau == 1) cout << tu << endl;
        else cout << tu << "/" << mau << endl;
    }
};

int main() {
    freopen("PHANSO.INP", "r", stdin);
    freopen("PHANSO.OUT", "w", stdout);

    long long t1, m1, t2, m2;
    if (cin >> t1 >> m1 >> t2 >> m2) {
        PhanSo ps1(t1, m1), ps2(t2, m2);
        PhanSo tong = ps1.cong(ps2);
        tong.in_ket_qua();
    }
    return 0;
}

Bài 6: Tìm số xuất hiện nhiều nhất (TIMSO)

Bài toán: Tìm số xuất hiện nhiều nhất trong dãy. Nếu có nhiều số cùng số lần xuất hiện, chọn số nhỏ nhất.

• Thời gian chạy: 1.0 giây

• Dữ liệu vào (TIMSO.INP): * Dòng 1: $N$ (N ≤ 10^5).

  • Dòng 2: $N$ số nguyên.

• Dữ liệu ra (TIMSO.OUT): Giá trị số tìm được và số lần xuất hiện.

Ví dụ:

• Input (TIMSO.INP):

  7

  2 3 5 2 3 8 2

• Output (TIMSO.OUT): 2 3

Code C++ tham khảo:

#include <iostream>
#include <map>
using namespace std;

int main() {
    freopen("TIMSO.INP", "r", stdin);
    freopen("TIMSO.OUT", "w", stdout);

    int n;
    if (cin >> n) {
        map<int, int> bo_dem;
        int so_nhap;
        
        for (int i = 0; i < n; i++) {
            cin >> so_nhap;
            bo_dem[so_nhap]++; 
        }

        int max_tan_suat = 0;
        int gia_tri_toi_uu = 0;

        for (auto phan_tu : bo_dem) {
            if (phan_tu.second > max_tan_suat) {
                max_tan_suat = phan_tu.second;
                gia_tri_toi_uu = phan_tu.first;
            }
        }

        cout << gia_tri_toi_uu << " " << max_tan_suat << endl;
    }
    return 0;
}

Tags: #HocLapTrinhC #LapTrinhC++ #ThiHSGTinHoc #CodeC++CoBan #GiaiThuatC++ #DeThiTinHoc #TuHocC++

1. Giới thiệu về C++

C++ là ngôn ngữ lập trình được phát triển bởi Bjarne Stroustrup vào năm 1985 dựa trên ngôn ngữ C. Đây là một trong những ngôn ngữ mạnh mẽ và phổ biến nhất hiện nay, được sử dụng để phát triển:

• Phần mềm máy tính
• Game
• Hệ điều hành
• Trí tuệ nhân tạo (AI)
• Ứng dụng tài chính
• Phần mềm nhúng

Ưu điểm của C++

• Tốc độ xử lý nhanh.
• Hỗ trợ lập trình hướng đối tượng (OOP).
• Có thư viện phong phú.
• Được sử dụng rộng rãi trong công nghiệp.

CHƯƠNG 1: LÀM QUEN VỚI C++

1. Cấu trúc chương trình C++

Ví dụ:

#include <iostream>
using namespace std;

int main() {
    cout << "Xin chao C++";
    return 0;
}

Giải thích

• #include <iostream>: Thư viện nhập xuất.
• using namespace std;: Sử dụng không gian tên chuẩn.
• main(): Hàm chính của chương trình.
• cout: Xuất dữ liệu ra màn hình.
• return 0;: Kết thúc chương trình.

2. Biến và kiểu dữ liệu

Các kiểu dữ liệu cơ bản

Ví dụ

int age = 18;
float diem = 8.5;
char grade = 'A';
string name = "Tan";

Bài tập

Bài 1

Nhập tên và tuổi của một người rồi xuất ra màn hình.

Ví dụ

Input

Tan
18

Output

Ten: Tan
Tuoi: 18

CHƯƠNG 2: CÂU LỆNH ĐIỀU KIỆN

1. Câu lệnh if

if (dieu_kien)
{
    // câu lệnh
}

Ví dụ:

int a;

cin >> a;

if (a > 0)
{
    cout << "So duong";
}

2. Câu lệnh if…else

if(a % 2 == 0)
{
    cout << "So chan";
}
else
{
    cout << "So le";
}

3. Câu lệnh switch

switch(n)
{
    case 1:
        cout<<"Mot";
        break;

    case 2:
        cout<<"Hai";
        break;

    default:
        cout<<"Khong hop le";
}

Bài tập

Bài 2

Nhập số nguyên n.

• Nếu n > 0 in “So duong”
• Nếu n < 0 in “So am”
• Nếu n = 0 in “So 0”

CHƯƠNG 3: VÒNG LẶP

1. Vòng lặp for

for(int i=1;i<=10;i++)
{
    cout<<i<<" ";
}

Kết quả:

1 2 3 4 5 6 7 8 9 10

2. Vòng lặp while

int i=1;

while(i<=5)
{
    cout<<i<<" ";
    i++;
}

Bài tập

Bài 3

Tính tổng:

S = 1 + 2 + 3 + ... + n

Ví dụ:

Input

5

Output

15

CHƯƠNG 4: HÀM (FUNCTION)

Hàm giúp chia chương trình thành các phần nhỏ.

Ví dụ:

int tong(int a, int b)
{
    return a+b;
}

int main()
{
    cout<<tong(3,5);

    return 0;
}

Kết quả:

8

Bài tập

Viết hàm:

1. Tính giai thừa n!
2. Kiểm tra số nguyên tố.
3. Tính UCLN của hai số.

CHƯƠNG 5: MẢNG (ARRAY)

Khai báo

int a[100];

Nhập mảng

int n;

cin>>n;

for(int i=0;i<n;i++)
{
    cin>>a[i];
}

Xuất mảng

for(int i=0;i<n;i++)
{
    cout<<a[i]<<" ";
}

Bài tập

Cho mảng n số nguyên.

Hãy:

• Tính tổng các phần tử.
• Tìm số lớn nhất.
• Tìm số nhỏ nhất.
• Sắp xếp tăng dần.

CHƯƠNG 6: CHUỖI (STRING)

Ví dụ:

string s;

getline(cin,s);

cout<<s;

Một số hàm thường dùng

s.length();      // độ dài
s.substr(0,3);   // cắt chuỗi
s.find("abc");   // tìm chuỗi

Bài tập

Nhập một chuỗi.

1. Đếm số ký tự.
2. Đếm số chữ cái.
3. Đếm số từ.
4. Đảo ngược chuỗi.

CHƯƠNG 7: CON TRỎ

Con trỏ là biến lưu địa chỉ của biến khác.

Ví dụ:

int a=10;

int *p=&a;

cout<<a<<endl;
cout<<&a<<endl;
cout<<p<<endl;
cout<<*p<<endl;

CHƯƠNG 8: LẬP TRÌNH HƯỚNG ĐỐI TƯỢNG (OOP)

1. Class

class Student
{
public:

    string name;
    int age;

    void display()
    {
        cout<<name<<" "<<age;
    }
};

2. Tạo đối tượng

Student s;

s.name="Tan";

s.age=18;

s.display();

Các khái niệm OOP quan trọng

Encapsulation (Đóng gói)

Ẩn dữ liệu bằng từ khóa:

private

Inheritance (Kế thừa)

class Animal
{
};

class Dog : public Animal
{
};

Polymorphism (Đa hình)

Cho phép cùng tên hàm nhưng hoạt động khác nhau.

Abstraction (Trừu tượng)

Ẩn chi tiết cài đặt và chỉ cung cấp chức năng cần thiết.

CHƯƠNG 9: THƯ VIỆN STL

STL (Standard Template Library) là thư viện cực kỳ quan trọng trong C++.

Vector

vector<int> a;

a.push_back(10);

a.push_back(20);

cout<<a.size();

Stack

stack<int> st;

st.push(1);

st.push(2);

st.pop();

Queue

queue<int> q;

q.push(5);

q.push(10);

q.pop();

Map

map<string,int> mp;

mp["Tan"]=18;

cout<<mp["Tan"];

CHƯƠNG 10: THUẬT TOÁN NÂNG CAO

Sau khi học xong C++ cơ bản, bạn nên học:

1. Đệ quy (Recursion)

Ví dụ tính giai thừa:

int gt(int n)
{
    if(n==0)
        return 1;

    return n*gt(n-1);
}

2. Sắp xếp

• Bubble Sort
• Selection Sort
• Insertion Sort
• Merge Sort
• Quick Sort

3. Tìm kiếm

• Linear Search
• Binary Search

4. Quy hoạch động (Dynamic Programming)

Ví dụ:

• Dãy Fibonacci
• Balo 0/1
• Đường đi ngắn nhất

BÀI TẬP TỔNG HỢP

Bài 1

Nhập n.

Tính:

S = 1² + 2² + 3² + ... + n²

Bài 2

Nhập mảng n số nguyên.

In ra:

• Số lớn nhất
• Số nhỏ nhất
• Trung bình cộng
• Mảng sau khi sắp xếp

Bài 3

Viết chương trình quản lý sinh viên gồm:

• Mã sinh viên
• Họ tên
• Tuổi
• Điểm trung bình

Chức năng:

1. Thêm sinh viên
2. Xóa sinh viên
3. Sửa thông tin
4. Tìm kiếm
5. Sắp xếp theo điểm
6. Lưu dữ liệu ra file

LỘ TRÌNH HỌC C++ ĐỀ XUẤT

Tuần 1

• Biến
• Kiểu dữ liệu
• if, switch
• for, while

Tuần 2

• Hàm
• Mảng
• Chuỗi
• Con trỏ

Tuần 3

• Struct
• Class
• OOP

Tuần 4

• Vector
• Stack
• Queue
• Map
• Thuật toán cơ bản

Tuần 5 trở đi

• Đệ quy
• Thuật toán nâng cao
• Quy hoạch động
• Giải bài tập trên các trang OJ như Codeforces, LeetCode, VNOI.

Kết luận

C++ là ngôn ngữ mạnh mẽ, phù hợp cho cả người mới bắt đầu và lập trình viên chuyên nghiệp. Hãy học theo thứ tự:

Cơ bản → Hàm → Mảng → Chuỗi → Con trỏ → OOP → STL → Thuật toán → Dự án thực tế

Kiên trì luyện tập mỗi ngày sẽ giúp bạn thành thạo C++ và có nền tảng tốt để học các lĩnh vực như AI, lập trình game, phát triển phần mềm và thi lập trình cạnh tranh.

Khóa Học Tin Học Online Thầy Dân: Luyện Thi Chuyên Tin & Tin Văn Phòng Cấp Tốc

Bạn đang tìm kiếm một lộ trình học Tin học bài bản để thi vào các trường chuyên? Bạn muốn nâng cao kỹ năng Tin học văn phòng để tự tin đi làm nhưng lại không có nhiều thời gian? Khóa học Tin học Online của Thầy Dân chính là giải pháp hoàn hảo dành cho bạn.

Với phương pháp giảng dạy tận tâm, dễ hiểu và lộ trình cá nhân hóa, Thầy Dân giúp học viên làm chủ kiến thức từ cơ bản đến nâng cao ngay tại nhà.

Khóa học tin học văn phòng online miễn phí

1. Tại sao nên đăng ký khóa học Tin học Online của Thầy Dân?

Trong thời đại công nghệ số, việc học online mang lại những ưu thế vượt trội. Khi đăng ký học cùng Thầy Dân, học viên sẽ nhận được 5 lợi ích vàng:

• Tiết kiệm thời gian và học phí: Không cần di chuyển xa, giảm thiểu chi phí đi lại nhưng vẫn đảm bảo chất lượng kiến thức như học trực tiếp.

• Tặng kèm tài liệu độc quyền: Bộ giáo trình và bài tập được Thầy Dân biên soạn riêng, sát với thực tế và các kỳ thi.

• Luyện thi vào lớp 10 chuyên Tin tại nhà: Lộ trình ôn luyện bài bản, tập trung vào các dạng đề thi của các trường chuyên trọng điểm.

• Ôn thi học sinh giỏi cấp Huyện, Tỉnh: Hỗ trợ học viên bồi dưỡng kiến thức nâng cao, tư duy lập trình để chinh phục các giải thưởng lớn.

• Học Tin học văn phòng thực chiến: Trang bị kỹ năng Word, Excel, PowerPoint chuyên sâu để ứng dụng ngay vào công việc văn phòng.

Tin học lớp 5

2. Các chương trình đào tạo trọng điểm

Luyện thi lớp 10 Chuyên Tin & Học sinh giỏi

Đây là thế mạnh của Thầy Dân. Chương trình được thiết kế giúp học viên nắm vững thuật toán, tư duy logic và cách xử lý các dạng bài khó trong đề thi học sinh giỏi và kỳ thi tuyển sinh lớp 10 trường chuyên.

73 Đề thi HSG Tin học Python THCS cấp tỉnh Tiền Giang có ĐÁP ÁN (Mới & Chọn Lọc)

Tin học văn phòng cho người đi làm

Khóa học tập trung vào các kỹ năng thực tế mà doanh nghiệp cần. Giúp bạn xử lý văn bản chuyên nghiệp, quản lý dữ liệu hiệu quả bằng Excel và tạo ra những bản thuyết trình ấn tượng.

Khoá luyện thi Chuyên Tin Tiền Giang

3. Hình thức học và Cam kết chất lượng

• Khóa học tin học online thầy Dân chuyên luyện thi tin học văn phòng cấp tốc (MOS, IC3) và luyện thi chuyên tin, tập trung vào kỹ năng thực chiến, giải đề và thao tác máy tính nhanh.
• Chương trình cá nhân hóa, dạy 1:1, phù hợp cho người đi làm, học sinh, sinh viên cần chứng chỉ gấp hoặc nâng cao kỹ năng tin học từ cơ bản đến nâng cao.

Đặc điểm khóa học:

• • Tin học văn phòng: Đào tạo cấp tốc Word, Excel, PowerPoint, kỹ năng xử lý dữ liệu và soạn thảo văn bản chuyên nghiệp.
  • Luyện thi: Ôn luyện các chứng chỉ quốc tế MOS, IC3, đáp ứng đầu ra chuẩn quốc tế.
  • Hình thức: Học online 1:1 hoặc nhóm nhỏ, linh hoạt thời gian, tương tác trực tiếp với giảng viên.
  • Cam kết: Tập trung vào thực hành, “cầm tay chỉ việc”, đảm bảo vững kiến thức và kỹ năng sau khóa học.

• Nhận học viên thường xuyên: Bạn có thể đăng ký và bắt đầu học ngay mà không phải chờ đợi mở lớp.

• Tương tác trực tiếp: Dù là học online, học viên vẫn được thầy hỗ trợ giải đáp thắc mắc nhanh chóng qua Zalo và các nền tảng hỗ trợ.

• Hình ảnh thực tế: Các lớp học của Thầy Dân luôn nhận được sự tin tưởng của đông đảo phụ huynh và học sinh (như hình ảnh các lớp học trực tiếp đầy ắp học viên là minh chứng cho uy tín của thầy).

Tự học tin học văn phòng tài nhà

4. Liên hệ đăng ký khóa học ngay hôm nay

Đừng để rào cản về địa lý hay thời gian ngăn cản bước tiến của bạn. Hãy liên hệ ngay với Thầy Dân để được tư vấn lộ trình học phù hợp nhất với mục tiêu của bạn.

• Giáo viên: Thầy Dân

• Hotline/Zalo: 0937.179.278

• Dịch vụ: Đào tạo Tin học Online/Offline, luyện thi chuyên, luyện thi HSG, đào tạo nghề văn phòng.

Học Tin học không khó – Nếu bạn có lộ trình đúng và người thầy tận tâm!

Tự học Excel dành cho người mới bắt đầu

❓ CÂU HỎI THƯỜNG GẶP (FAQ) – TIN HỌC THẦY DÂN

1. Khóa học của Thầy Dân dành cho đối tượng nào?

Khóa học được thiết kế đa dạng cho nhiều đối tượng:

• Học sinh cấp 2, cấp 3: Ôn thi Học sinh giỏi (HSG) cấp Huyện/Tỉnh và luyện thi vào lớp 10 chuyên Tin.

• Người đi làm/Sinh viên: Cần học Tin học văn phòng (Word, Excel, PowerPoint) cấp tốc để phục vụ công việc.

• Người mới bắt đầu: Muốn làm quen với máy tính bài bản từ đầu.

2. Học Online có đảm bảo chất lượng bằng học trực tiếp không?

Hoàn toàn đảm bảo! Chương trình Online của Thầy Dân được tối ưu hóa:

• Học viên được tương tác trực tiếp, giải đáp thắc mắc qua Zalo/Ultraview.

• Lộ trình học cá nhân hóa theo năng lực từng người.

• Hệ thống bài tập thực hành sát với đề thi và thực tế công sở.

3. Tôi có được tặng tài liệu khi đăng ký không?

Có. Tất cả học viên khi đăng ký đều được tặng kèm bộ Tài liệu độc quyền do chính Thầy Dân biên soạn. Bộ tài liệu bao gồm lý thuyết trọng tâm, các dạng bài tập thực hành và ngân hàng đề thi các năm.

4. Lịch học và thời gian khai giảng như thế nào?

Thầy Dân nhận học viên thường xuyên. Bạn không cần phải chờ đợi đủ lớp mới bắt đầu. Thời gian học linh hoạt, phù hợp cho cả học sinh đang đi học chính khóa và người đi làm bận rộn.

5. Khóa luyện thi Chuyên Tin lớp 10 tập trung vào những gì?

Khóa học sẽ tập trung vào:

• Rèn luyện tư duy lập trình (Pascal, C++, Python… tùy theo đề thi địa phương).

• Xử lý các thuật toán nâng cao thường xuất hiện trong đề thi chuyên.

• Kỹ năng giải đề và tối ưu thời gian làm bài để đạt điểm tối đa.

6. Tôi muốn học để đi làm văn phòng thì mất bao lâu?

Tùy vào kỹ năng hiện tại, thông thường chỉ sau 4 – 8 tuần, bạn sẽ làm chủ được các kỹ năng văn phòng cần thiết. Thầy tập trung dạy “thực chiến”, học đến đâu dùng được ngay đến đó, không dạy lý thuyết suông.

• Luyện Thi Chuyên Tin: Tập trung kiến thức chuyên tin từ A-Z (ngôn ngữ lập trình, thuật toán, tư duy tin học).
• Tin Học Văn Phòng Cấp Tốc: Đào tạo kỹ năng Word, Excel, PowerPoint nhanh chóng, áp dụng.
• Hình thức: Học online tiện lợi, phù hợp cho người đi làm hoặc học sinh cần ôn thi.
• Nội dung: Được thiết kế từ cơ bản đến nâng cao, đảm bảo học viên thành thạo kỹ

7. Cách thức đăng ký và đóng học phí như thế nào?

Bạn có thể liên hệ trực tiếp với Thầy qua các kênh sau để được tư vấn và nhận báo giá ưu đãi:

• Số điện thoại / Zalo: 0937.179.278

• Hình thức đóng phí: Chuyển khoản ngân hàng hoặc nộp trực tiếp tại cơ sở (nếu học offline).

Đạt giải 3 học sinh giỏi tin học cấp tỉnh

Nếu bạn thấy hay ! xin bạn 1 phút ! vui lòng đánh giá 5 sao cho trang website của chúng tôi ! để có động lực làm thêm nhiều bài hay nữa ! cảm ơn quý khách nhé !

2 Khóa Học Tin Học Online Thầy Dân Luyện Thi Chuyên Tin Tin Văn Phòng Cấp Tốc

🚀 Giải Chi Tiết Đề Thi HSG Tin Học THCS Bình Phước (Có Code Python Chuẩn) – Dễ Hiểu, Lên Tay Nhanh

Bạn đang ôn thi học sinh giỏi Tin học cấp tỉnh? Bài viết này tổng hợp và giải chi tiết các bài trong đề HSG Tin học THCS Bình Phước, kèm code Python chuẩn thi, giải thích dễ hiểu và tối ưu để bạn áp dụng ngay.

Hướng dẫn Giải đề thi học sinh giỏi tin học lớp 9 THCS Tỉnh Bình Phước 2019 – 2020 mới cập nhật ngày 11/4/2026

GIẢI BÀI 1: ĐIỂM TRUNG BÌNH

import sys

sys.stdin = open("DIEMTB.INP", "r")
sys.stdout = open("DIEMTB.OUT", "w")

# đọc dữ liệu
x, y = map(int, input().split())

# tính điểm trung bình
dtb = (3 * x + y) / 4

# kiểm tra
if dtb >= 5:
    print(1)
else:
    print(0)

GIẢI BÀI 2: TÍNH TỔNG

🧠 Phân tích

Yêu cầu:
👉 Tính tổng M chữ số tận cùng của số N

Ví dụ:

• N = 25487, M = 2 → lấy 2 chữ số cuối: 8 + 7 = 15
• N = 5876512, M = 3 → lấy: 5 + 1 + 2 = 8

⚡ Cách làm

Có 2 cách:

✅ Cách 1: Dùng chuỗi (dễ hiểu nhất)

• Đổi N → string
• Lấy M ký tự cuối
• Cộng lại

💻 Code Python (chuẩn thi)

import sys

sys.stdin = open("TINHTONG.INP", "r")
sys.stdout = open("TINHTONG.OUT", "w")

# đọc dữ liệu
n = input().strip()
m = int(input())

# lấy m chữ số cuối
last_digits = n[-m:]

# tính tổng
tong = 0
for c in last_digits:
    tong += int(c)

print(tong)

🚀 Cách 2: Dùng toán học (pro hơn, không cần string)

👉 Ý tưởng:

• Lấy từng chữ số cuối bằng % 10
• Lặp M lần

💻 Code:

import sys

sys.stdin = open("TINHTONG.INP", "r")
sys.stdout = open("TINHTONG.OUT", "w")

n = int(input())
m = int(input())

tong = 0

for _ in range(m):
    tong += n % 10
    n //= 10

print(tong)

🎯 So sánh

🔥 Lưu ý quan trọng

• Nếu M > số chữ số của N → vẫn chạy đúng (lấy hết số)
• Độ phức tạp: O(M) → rất nhanh

GIẢI BÀI 3: BỘ BA SỐ LỚN NHẤT

Bài này là dạng trượt cửa sổ (Sliding Window) – cực kỳ hay trong HSG 🔥

🧠 Phân tích

Ta cần:

• Xét mọi bộ 3 số liên tiếp:

  ai+ai+1+ai+2a_i + a_{i+1} + a_{i+2}ai​+ai+1​+ai+2​

• Tìm tổng lớn nhất
• Nếu nhiều bộ → chọn chỉ số nhỏ nhất

⚡ Ý tưởng tối ưu

👉 Không cần tính lại từ đầu mỗi lần
→ Dùng cửa sổ trượt

• Ban đầu:
  sum = a[0] + a[1] + a[2]

• Sau đó:

  sum = sum – a[i-1] + a[i+2]

⏱ Độ phức tạp: O(n) (rất nhanh)

import sys

# đọc/ghi file
sys.stdin = open("BOMAX.INP", "r")
sys.stdout = open("BOMAX.OUT", "w")

# nhập dữ liệu
n = int(input())
day = list(map(int, input().split()))

# tính tổng 3 phần tử đầu tiên
tong_hien_tai = day[0] + day[1] + day[2]
tong_lon_nhat = tong_hien_tai

vi_tri_bat_dau = 0  # vị trí bắt đầu (0-based)

# duyệt các bộ còn lại
for i in range(1, n - 2):
    # cập nhật tổng bằng cửa sổ trượt
    tong_hien_tai = tong_hien_tai - day[i - 1] + day[i + 2]
    
    # nếu tìm được tổng lớn hơn thì cập nhật
    if tong_hien_tai > tong_lon_nhat:
        tong_lon_nhat = tong_hien_tai
        vi_tri_bat_dau = i

# in kết quả (đổi sang chỉ số 1-based)
print(tong_lon_nhat)
print(vi_tri_bat_dau + 1, vi_tri_bat_dau + 3)

📌 Ví dụ

Input:

Các bộ:

• (2,8,4) = 14
• (8,4,6) = 18 ✅
• (4,6,3) = 13

👉 Output:

🚀 Lưu ý quan trọng (hay bị sai)

• Chỉ update khi > (không phải ≥)
  → để giữ chỉ số nhỏ nhất
• In ra chỉ số 1-based

🔥 Nâng cấp (chuẩn HSG thật)

Bạn có thể gặp biến thể:

• Bộ k phần tử lớn nhất (k bất kỳ)
• Không liên tiếp → dùng DP
• Tổng lớn nhất nhưng ≤ X → khó hơn

🧠 Giải thích ngắn gọn

• tong_hien_tai: tổng của 3 số liên tiếp đang xét
• tong_lon_nhat: tổng lớn nhất tìm được
• vi_tri_bat_dau: vị trí đầu của bộ 3

👉 Mỗi lần:

⚠️ Lỗi hay gặp

• Dùng >= → sai (phải dùng > để lấy vị trí nhỏ nhất)
• Quên đổi sang 1-based
• Sai chỉ số i + 2

GIẢI BÀI 4: MẬT KHẨU

🧠 Bài: MẬT KHẨU

📌 Yêu cầu (suy ra từ đề)

• Cho xâu S (độ dài ≤ 255)
• Tìm một số nguyên P từ các chữ số trong S
• Nếu:
  • Không có chữ số nào
  • Hoặc chỉ toàn số 0
    👉 thì P = 0

🎯 Cách hiểu chuẩn (dạng rất hay thi)

👉 Lấy tất cả chữ số trong chuỗi S, ghép lại thành số lớn nhất có thể

⚡ Ví dụ dễ hiểu

import sys

sys.stdin = open("MATKHAU.INP", "r")
sys.stdout = open("MATKHAU.OUT", "w")

# nhập xâu
s = input().strip()

# lấy các chữ số
chu_so = []

for c in s:
    if c.isdigit():
        chu_so.append(c)

# nếu không có chữ số
if len(chu_so) == 0:
    print(0)
else:
    # sắp xếp giảm dần để tạo số lớn nhất
    chu_so.sort(reverse=True)
    
    # ghép lại thành số
    ket_qua = "".join(chu_so)
    
    # nếu toàn số 0
    if int(ket_qua) == 0:
        print(0)
    else:
        print(int(ket_qua))

🔥 Giải thích nhanh

• isdigit() → kiểm tra có phải số không
• sort(reverse=True) → tạo số lớn nhất
• "".join() → ghép lại

⚠️ Lưu ý thi

• Không dùng int sớm → dễ lỗi với số lớn
• Xử lý riêng trường hợp toàn số 0

Nếu bạn thấy hay ! xin bạn 1 phút ! vui lòng đánh giá 5 sao cho trang website của chúng tôi ! để có động lực làm thêm nhiều bài hay nữa ! cảm ơn quý khách nhé !

2 Khóa Học Tin Học Online Thầy Dân Luyện Thi Chuyên Tin Tin Văn Phòng Cấp Tốc

Bạn đang tìm kiếm nguồn tài liệu ôn thi học sinh giỏi Tin học lớp 9 để chuẩn bị cho kỳ thi cấp huyện, cấp tỉnh sắp tới? Việc luyện đề từ các tỉnh thành khác nhau là phương pháp hiệu quả nhất để làm quen với cấu trúc đề, các dạng bài lập trình khó và cách tối ưu thuật toán.

Bài viết này tổng hợp 76 đề thi HSG Tin 9 cấp tỉnh có đáp án chi tiết, giúp các bạn học sinh tự tin chinh phục giải cao.

Các đề ôn thi để chuẩn bị thi Cấp XÃ thì các em vào đường dẫn phía dưới để tham khảo giúp thầy nhé!

1. Giải đề 1 và đáp án thi Học sinh giỏi tin học Python C++ THCS có tài liệu ôn thi
2. Giải đề 2 và đáp án thi Học sinh giỏi tin học Python C++ THCS có tài liệu ôn thi
3. Giải đề 3 thi học sinh giỏi tin học lập trình Python có đáp án
4. Giải đề 4 ôn thi học sinh giỏi Tin Học THCS lập trình Python có đáp án
5. Giải đề 5 và đáp án thi HSG Tin Python có số Pell.
6. Giải đề 6 và đáp án bồi dưỡng học sinh giỏi tin 10 có số Armstrong
7. Giải đề 7 và đáp án  thi học sinh giỏi tin học 10 Python có số Collatz
8. Giải đề 8 trong 20 đề Bồi dưỡng học sinh giỏi Tin học lớp 9 có số Kaprekar.
9. Giải đề 9 thi HSG Tin học lớp 8 lập trình Python có số Happy
10. Giải đề 10 thi tin học trẻ THPT có bài  In các xâu con trong xâu s.

1. Tại sao cần luyện đề thi HSG Tin học 9 các năm trước?

Kỳ thi học sinh giỏi Tin học lớp 9 thường tập trung vào kỹ năng giải quyết vấn đề thông qua lập trình (Pascal, C++, hoặc Python). Việc luyện tập với bộ 76 đề thi HSG Tin 9 sẽ giúp bạn:

• Nắm vững cấu trúc đề: Thông thường gồm 3-4 bài với độ khó tăng dần (bài toán số học, xử lý xâu, quy hoạch động, đồ thị cơ bản).

• Rèn luyện tư duy thuật toán: Tiếp cận với nhiều dạng bài mới lạ từ các tỉnh thành có phong trào Tin học mạnh như Nghệ An, Thanh Hóa, Hà Nội, Nam Định…

• Kỹ năng trình bày: Xem đáp án chi tiết giúp bạn hiểu cách chấm điểm và tối ưu mã nguồn để đạt điểm tối đa.

2. Cấu trúc bộ đề thi HSG Tin 9 trong bộ sưu tập này

Bộ tài liệu 76 đề thi HSG Tin 9 cấp tỉnh có đáp án được chúng tôi sưu tầm và biên soạn lại một cách khoa học:

• Đa dạng ngôn ngữ: Hỗ trợ lời giải bằng Pascal, C++ (phổ biến nhất) và một số đề mới có hướng dẫn bằng Python.

• Phân loại theo chuyên đề: * Bài tập về số học (Số nguyên tố, số chính phương, số đặc biệt).

  • Xử lý xâu ký tự và tệp dữ liệu.

  • Thuật toán tìm kiếm và sắp xếp.

  • Kỹ thuật đệ quy và quy hoạch động cơ bản.

• Có đáp án và hướng dẫn chấm: Giúp học sinh và giáo viên dễ dàng đối chiếu kết quả.

3. Danh sách một số đề thi tiêu biểu trong bộ 76 đề

Dưới đây là một số đề thi “hot” nhất trong bộ sưu tập mà bạn không nên bỏ qua:

1. Đề thi HSG Tin 9 tỉnh Nghệ An (Bảng A, B).

2. Đề thi HSG Tin 9 tỉnh Thanh Hóa (Đầy đủ các năm).

3. Đề thi chọn đội tuyển HSG lớp 9 TP. Hà Nội.

4. Đề thi giao lưu học sinh giỏi các tỉnh đồng bằng Bắc Bộ.

5. Đề thi tuyển sinh vào lớp 10 chuyên Tin (Phần tự chọn HSG 9).

4. Link tải 76 Đề thi HSG Tin 9 cấp Tỉnh Có đáp án (Full File Word/PDF)

Để hỗ trợ các bạn ôn tập tốt nhất, chúng tôi đã đóng gói toàn bộ 76 đề thi vào một thư mục duy nhất. Bạn có thể tải về hoàn toàn miễn phí theo đường link dưới đây:

[Link Tải Xuống 76 Đề Thi HSG Tin 9 Có Đáp Án Tại Đây]

(Lưu ý: Nếu link lỗi, vui lòng để lại bình luận phía dưới để admin cập nhật ngay lập tức).

5. Kinh nghiệm đạt điểm cao trong kỳ thi HSG Tin học 9

Ngoài việc luyện đề, bạn cần lưu ý:

1. Đọc kỹ đề bài: Xác định rõ ràng Input, Output và các giới hạn (Constraints) của đề.

2. Quản lý thời gian: Đừng quá sa đà vào bài khó, hãy hoàn thành chắc chắn các bài dễ để lấy điểm tuyệt đối trước.

3. Kiểm tra kỹ các trường hợp biên: Test thử với dữ liệu nhỏ nhất, lớn nhất hoặc các trường hợp đặc biệt (n = 0, n = 1…).

4. Cập nhật ngôn ngữ: Hiện nay nhiều tỉnh đã cho phép sử dụng C++11, C++17 và Python, hãy tận dụng các thư viện mạnh mẽ để rút ngắn thời gian làm bài.

Lời kết: Hy vọng bộ tài liệu 76 đề thi HSG Tin 9 cấp tỉnh có đáp án này sẽ là hành trang vững chắc giúp các bạn đạt kết quả cao trong kỳ thi sắp tới. Nếu thấy tài liệu hữu ích, hãy chia sẻ cho bạn bè cùng ôn tập nhé!

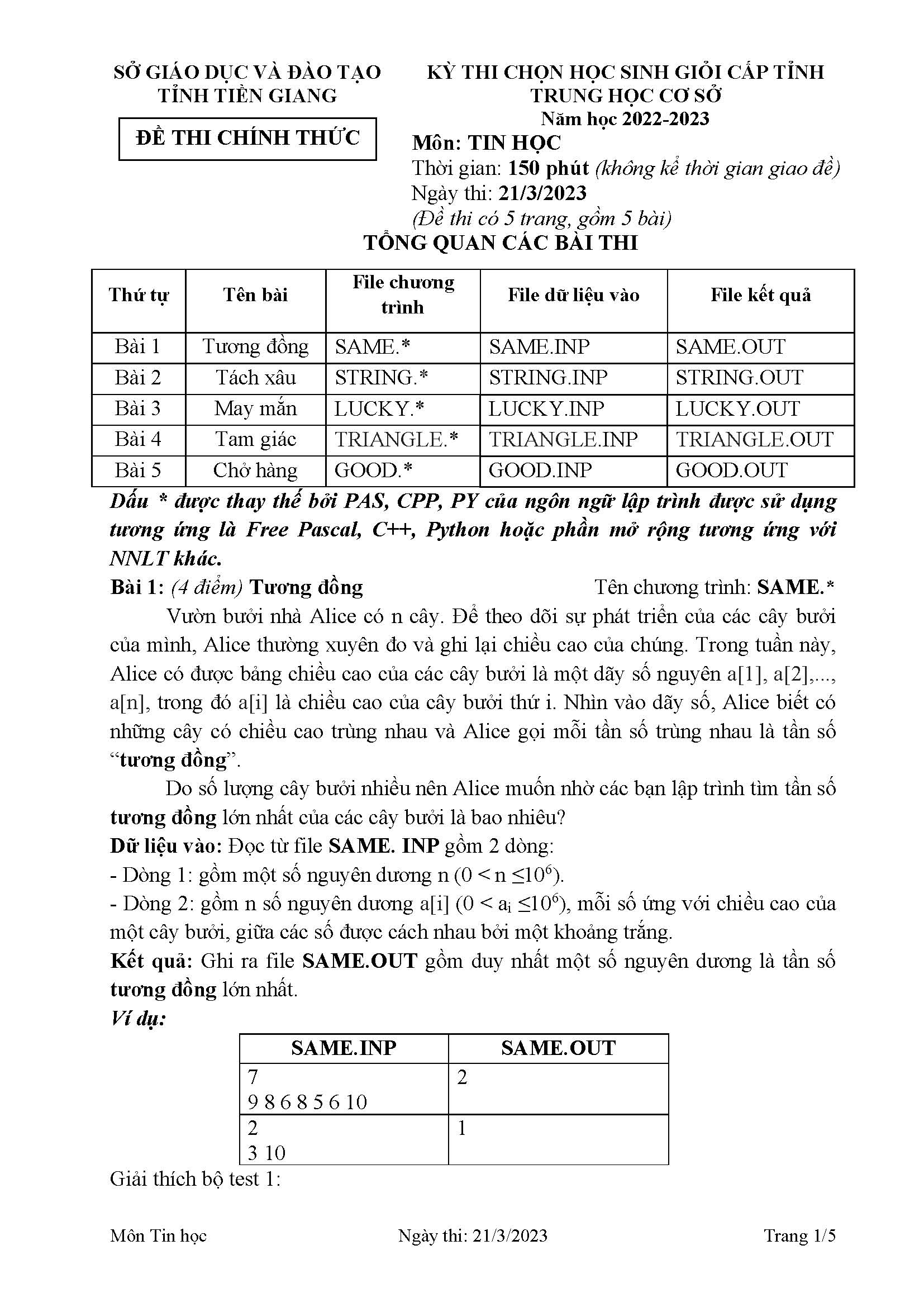
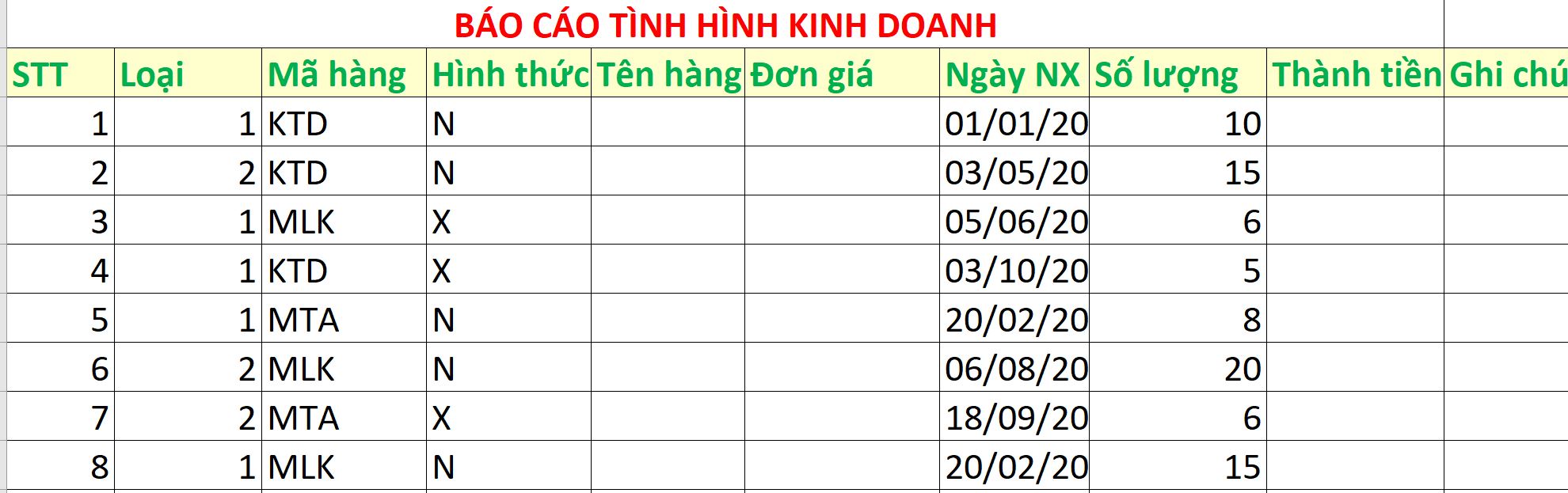
Giải đáp án bài 1: Tiền Điện

📌 Phân tích đề bài (tư duy giải)

• Có n hộ gia đình, mỗi hộ dùng aᵢ KWh điện.

• Giá điện chia 3 bậc:

👉 Với mỗi hộ, ta:

• Tính tiền bậc 1 (tối đa 100 KWh)

• Nếu còn → tính tiếp bậc 2 (tối đa 100 KWh)

• Nếu còn nữa → bậc 3

👉 Cộng tiền của tất cả các hộ lại.

🧠 Thuật toán

Với mỗi a (số KWh của 1 hộ):

• Nếu a ≤ 100
  → tiền = a * 2500

• Nếu 100 < a ≤ 200
  → tiền = 100*2500 + (a-100)*3000

• Nếu a > 200
  → tiền = 100*2500 + 100*3000 + (a-200)*3500

Code Python (chuẩn thi)

import sys

sys.stdin = open("ELCOST.INP", "r")
sys.stdout = open("ELCOST.OUT", "w")

# Đọc số hộ gia đình
n = int(sys.stdin.readline().strip())

# Đọc danh sách số KWh của các hộ
danh_sach = list(map(int, sys.stdin.readline().split()))

tong_tien = 0

for a in danh_sach:
    if a <= 100:
        tien = a * 2500
    elif a <= 200:
        tien = 100 * 2500 + (a - 100) * 3000
    else:
        tien = 100 * 2500 + 100 * 3000 + (a - 200) * 3500

    tong_tien += tien

# In kết quả
print(tong_tien)

✍️ Giải thích code ngắn gọn

• sys.stdin, sys.stdout → đúng chuẩn chấm bài tự động

• Duyệt từng hộ → tính tiền đúng theo bậc

• Cộng dồn vào tong_tien

• In ra một số nguyên duy nhất

⏱️ Phân tích độ phức tạp

• Vòng lặp chạy n lần

• Mỗi lần chỉ tính toán hằng số

👉 Độ phức tạp thời gian:

O(n)​

👉 Độ phức tạp bộ nhớ:

O(1) 

✅ Nhận xét theo chuẩn bài thi HSG

✔ Thuật toán đơn giản – đúng bản chất
✔ Không bị tràn số
✔ Chạy nhanh với n ≤ 10^4
✔ Dễ mở rộng nếu đề thêm bậc điện

Giải đáp án bài 2: Độ mạnh của xâu?

🔍 Phân tích đề bài

• Cho xâu s gồm:

  • Chữ cái thường a–z

  • Chữ số 0–9

• Không có khoảng trắng, không có ký tự đặc biệt

• Độ dài xâu ≤ 10^3

👉 Định nghĩa “độ mạnh của xâu”

Độ mạnh=(số kí tự phân biệt×(số lần xuất hiện nhiều nhất của 1kí tự )

🧠 Tư duy giải

Ta cần 2 thông tin:

1. Số kí tự phân biệt trong xâu

   • Chính là số lượng kí tự khác nhau

2. Số lần xuất hiện nhiều nhất

   • Tìm kí tự xuất hiện nhiều nhất

👉 Cách làm hiệu quả:

• Dùng dictionary (từ điển) để đếm số lần xuất hiện của từng kí tự

Code Python (chuẩn thi)

import sys

sys.stdin = open("STRONG.INP", "r")
sys.stdout = open("STRONG.OUT", "w")

# Đọc xâu
s = sys.stdin.readline().strip()

dem = {}

# Đếm số lần xuất hiện của từng kí tự
for ch in s:
    if ch in dem:
        dem[ch] += 1
    else:
        dem[ch] = 1

# Số kí tự phân biệt
so_ki_tu_phan_biet = len(dem)

# Số lần xuất hiện nhiều nhất
lan_xuat_hien_nhieu_nhat = max(dem.values())

# Độ mạnh của xâu
do_manh = so_ki_tu_phan_biet * lan_xuat_hien_nhieu_nhat

print(do_manh)

✍️ Giải thích code

• dem: từ điển lưu

  khóa = kí tự
  giá trị = số lần xuất hiện

• len(dem) → số kí tự phân biệt

• max(dem.values()) → tần suất lớn nhất

• Nhân 2 giá trị → độ mạnh

🧪 Kiểm tra bằng ví dụ đề bài

Ví dụ 1

• Kí tự phân biệt: {x, y, 1, z, 2, 0} → 6

• Kí tự xuất hiện nhiều nhất: y → 5 lần
  👉 Kết quả: 6 * 5 = 30

Ví dụ 2

• Phân biệt: 1

• Xuất hiện nhiều nhất: 5
  👉 Kết quả: 1 * 5 = 5

⏱️ Phân tích độ phức tạp

• Duyệt xâu độ dài n đúng 1 lần

👉 Thời gian:

O(n)​

👉 Bộ nhớ:

O(k)≤O(n)

(với k là số kí tự phân biệt)

✅ Nhận xét theo chuẩn HSG

✔ Thuật toán đơn giản – đúng bản chất
✔ Không dùng thư viện nâng cao
✔ Chạy rất nhanh với n ≤ 1000
✔ Dễ trình bày trong bài thi

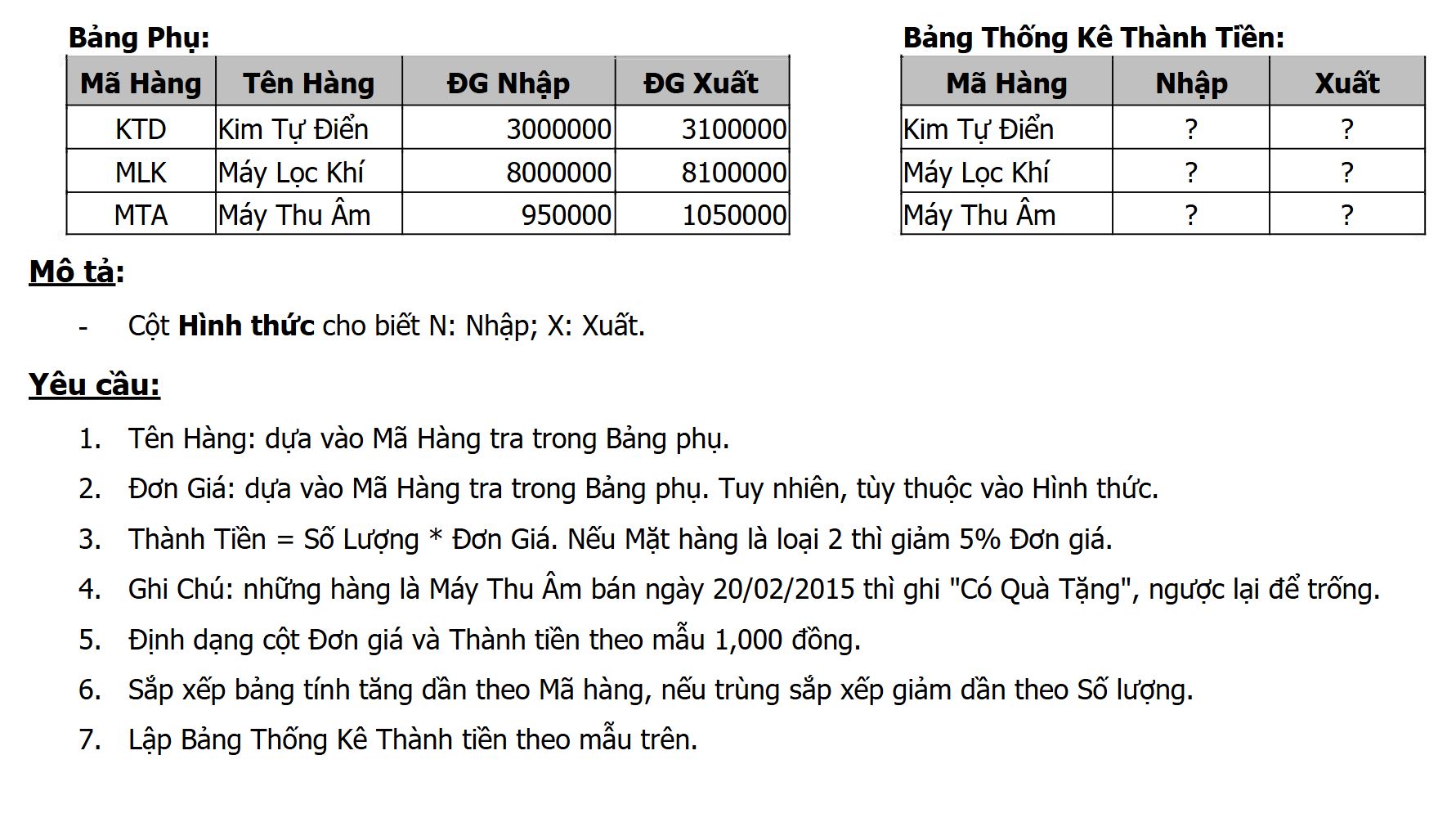
📌 Giải Đáp Án Bài 3: Tổng dòng cột (SUM)

🔍 Nội dung đề bài (tóm tắt)

• Cho ma trận a gồm m dòng và n cột.

• Tạo ma trận b theo công thức:

bij=(tổng doˋng i của a+tổng cột j của a)−aijb_{ij} ​

👉 Yêu cầu

Tìm giá trị nhỏ nhất trong ma trận b.

🧠 Tư duy giải (rất quan trọng – hay ra thi)

Nếu làm ngây thơ:

• Với mỗi ô (i, j) lại đi tính tổng dòng + tổng cột
  ❌ → chậm: O(m*n*(m+n)) → dễ TLE

👉 Cách làm đúng chuẩn HSG:

Bước 1:

• Tính tổng từng dòng → mảng tong_dong[i]

• Tính tổng từng cột → mảng tong_cot[j]

Bước 2:

• Với mỗi ô (i, j):

bij=tong_dong[i]+tong_cot[j]−a[i][j]

• Cập nhật giá trị nhỏ nhất

⚡ Không cần lưu ma trận b → tiết kiệm bộ nhớ

Code Python (chuẩn thi)

import sys

sys.stdin = open("SUM.INP", "r")
sys.stdout = open("SUM.OUT", "w")

# Đọc m, n
m, n = map(int, sys.stdin.readline().split())

# Đọc ma trận a
a = []
for _ in range(m):
    a.append(list(map(int, sys.stdin.readline().split())))

# Tính tổng từng dòng
tong_dong = [0] * m
for i in range(m):
    tong_dong[i] = sum(a[i])

# Tính tổng từng cột
tong_cot = [0] * n
for j in range(n):
    for i in range(m):
        tong_cot[j] += a[i][j]

# Tìm giá trị nhỏ nhất trong ma trận b
INF = 10**18
min_b = INF

for i in range(m):
    for j in range(n):
        b_ij = tong_dong[i] + tong_cot[j] - a[i][j]
        if b_ij < min_b:
            min_b = b_ij

print(min_b)

✍️ Giải thích code ngắn gọn

• tong_dong[i]: tổng dòng i

• tong_cot[j]: tổng cột j

• Với mỗi ô (i, j):

  • Áp dụng đúng công thức đề

  • Cập nhật min_b

• Không cần tạo ma trận b → tối ưu

⏱️ Phân tích độ phức tạp

• Tính tổng dòng: O(mn)

• Tính tổng cột: O(mn)

• Duyệt tìm min: O(mn)

👉 Tổng thời gian:

O(m×n)​

👉 Bộ nhớ:

O(m+n)​

✅ Nhận xét chuẩn HSG

✔ Áp dụng tiền xử lý (precompute)
✔ Tránh lặp thừa – tư duy tối ưu
✔ Phù hợp ma trận lớn
✔ Rất dễ ăn trọn 4 điểm

📌 Bài 4: Xâu lặp (SUBSTR)

🔍 Tóm tắt dạng bài (chuẩn đề Tiền Giang)

• Cho một xâu s (chỉ gồm chữ thường và chữ số, không có khoảng trắng)

• Xâu có độ dài ≤ 10^3

• Yêu cầu:
  👉 Tìm xâu con dài nhất xuất hiện ít nhất 2 lần trong s
  (cho phép chồng lấn)

Đây là dạng bài xâu lặp (longest repeated substring) – rất hay ra thi tỉnh.

🧠 Tư duy giải (đúng mức THCS – không dùng suffix array)

Vì |s| ≤ 1000, ta có thể dùng cách duyệt độ dài + kiểm tra trùng:

Ý tưởng:

1. Duyệt độ dài xâu con L từ lớn xuống nhỏ

2. Với mỗi L, duyệt tất cả các xâu con độ dài L

3. Dùng set để kiểm tra:

   • Nếu một xâu con đã xuất hiện → tìm được đáp án

4. Gặp độ dài lớn nhất đầu tiên → dừng luôn

👉 Cách này dễ cài, dễ trình bày, đủ nhanh cho đề tỉnh.

import sys

sys.stdin = open("SUBSTR.INP", "r")
sys.stdout = open("SUBSTR.OUT", "w")

s = sys.stdin.readline().strip()
n = len(s)

ket_qua = ""

# Duyệt độ dài xâu con từ lớn xuống nhỏ
for L in range(n - 1, 0, -1):
    tap_con = set()
    found = False

    for i in range(n - L + 1):
        sub = s[i:i+L]
        if sub in tap_con:
            ket_qua = sub
            found = True
            break
        tap_con.add(sub)

    if found:
        break

print(ket_qua)

✍️ Giải thích code

• Duyệt L từ n-1 → 1
  → đảm bảo lấy xâu dài nhất

• Với mỗi L:

  • Cắt các xâu con s[i:i+L]

  • Dùng set để kiểm tra trùng

• Khi phát hiện xâu lặp đầu tiên → in ra ngay

🧪 Ví dụ minh họa

Ví dụ

Các xâu lặp dài nhất:

• "ababa" xuất hiện 2 lần (chồng lấn)

👉 Kết quả:

⏱️ Phân tích độ phức tạp

• Duyệt độ dài: O(n)

• Với mỗi độ dài, duyệt xâu con: O(n)

• Cắt xâu + set: O(n)

👉 Tổng:

O(n3) (với n≤1000 là chấp nhận được)

👉 Bộ nhớ:

O(n2)​

✅ Nhận xét chuẩn HSG

✔ Không dùng thuật toán nâng cao (suffix array, Z, KMP)
✔ Dễ hiểu – dễ chép vào bài thi
✔ Đủ nhanh với dữ liệu đề tỉnh
✔ Trình bày rất “ăn điểm”

📌Giải Đáp Án Bài 5: Phần thưởng (GIFT)

🔍 Phân tích đề bài

• Có một dãy số là giá trị các phần thưởng (sắp theo một hàng).

• Mỗi phần thưởng có giá trị từ 1 đến 10^9.

• An muốn chọn một đoạn liên tiếp sao cho:
  👉 giá trị tăng dần liên tiếp
  (tức là: số sau lớn hơn số trước).

👉 Yêu cầu

Tìm độ dài lớn nhất của đoạn tăng dần liên tiếp.

📌 Lưu ý:

• Chỉ xét liên tiếp

• Không cần tăng đúng 1, chỉ cần lớn hơn

🧠 Tư duy giải (rất chuẩn thi)

Đây là bài:

Dãy con tăng liên tiếp dài nhất

👉 Không cần quy hoạch động phức tạp.

Ý tưởng:

• Duyệt từ trái sang phải

• Nếu a[i] > a[i-1]:

  • tăng độ dài đoạn hiện tại

• Ngược lại:

  • bắt đầu đoạn mới

• Luôn cập nhật độ dài lớn nhất

import sys

sys.stdin = open("GIFT.INP", "r")
sys.stdout = open("GIFT.OUT", "w")

# Đọc dãy phần thưởng
a = list(map(int, sys.stdin.readline().split()))
n = len(a)

# Nếu dãy rỗng (trường hợp hiếm)
if n == 0:
    print(0)
else:
    max_len = 1      # độ dài lớn nhất
    cur_len = 1      # độ dài đoạn hiện tại

    for i in range(1, n):
        if a[i] > a[i - 1]:
            cur_len += 1
        else:
            cur_len = 1

        if cur_len > max_len:
            max_len = cur_len

    print(max_len)

✍️ Giải thích code

• cur_len: độ dài đoạn tăng dần đang xét

• max_len: kết quả lớn nhất

• Khi gặp a[i] ≤ a[i-1]:

  • chuỗi tăng bị phá vỡ → reset cur_len = 1

• Duyệt xong là ra kết quả

🧪 Kiểm tra ví dụ đề bài

Ví dụ 1

Đoạn tăng dài nhất:

👉 Độ dài = 4

Ví dụ 2

Đoạn tăng dài nhất:

👉 Độ dài = 3

⏱️ Phân tích độ phức tạp

• Duyệt dãy 1 lần

👉 Thời gian:

O(n)​

👉 Bộ nhớ:

O(1)

✅ Nhận xét chuẩn HSG

✔ Bài điển hình – dễ ăn điểm
✔ Không cần mảng phụ
✔ Chạy rất nhanh dù n lớn
✔ Trình bày rõ ràng, sạch sẽ

Nếu bạn thấy hay ! xin bạn 1 phút ! vui lòng đánh giá 5 sao cho trang website của chúng tôi ! để có động lực làm thêm nhiều bài hay nữa ! cảm ơn quý khách nhé !

2 Khóa Học Tin Học Online Thầy Dân Luyện Thi Chuyên Tin Tin Văn Phòng Cấp Tốc

Khóa học Python online từ cơ bản đến nâng cao

Câu hỏi thường gặp về đề thi HSG Tin 9:

• Bộ 76 đề thi HSG Tin 9 này có kèm đáp án không? Dạ có, toàn bộ 76 đề thi trong bộ sưu tập đều đi kèm đáp án chi tiết và hướng dẫn giải thuật bằng các ngôn ngữ phổ biến như Pascal, C++, Python.

• Tài liệu này có bao gồm đề thi của những năm gần đây không? Có, bộ tài liệu được cập nhật các đề thi HSG cấp tỉnh mới nhất (năm học 2023-2024 và 2024-2025) từ các tỉnh thành có phong trào Tin học mạnh.

• Tôi có thể tải file Word để về chỉnh sửa không? Được ạ, link tải bao gồm cả định dạng PDF để xem nhanh và file Word (.docx) để quý thầy cô và các bạn học sinh tiện trích dẫn, chỉnh sửa đề bài.

• Luyện đề thi HSG Tin 9 nên tập trung vào ngôn ngữ nào? Hiện nay hầu hết các tỉnh đã chuyển sang C++ và Python. Tuy nhiên, bộ đề vẫn giữ lại các lời giải bằng Pascal cho những địa phương chưa thay đổi hình thức thi.

2 Khóa Học Tin Học Online Thầy Dân Luyện Thi Chuyên Tin Tin Văn Phòng Cấp Tốc

Phần 2: Tải ngay 200 Bài lập trình Python có lời giải cơ bản đến nâng cao PDF

Bạn đang bắt đầu hành trình chinh phục ngôn ngữ lập trình Python? Bạn đã nắm vững lý thuyết nhưng lại lúng túng khi bắt tay vào viết code thực tế? Tài liệu “200 Bài lập trình Python có lời giải cơ bản đến nâng cao PDF” chính là chiếc chìa khóa vàng giúp bạn chuyển hóa kiến thức thành kỹ năng thực chiến.

Phần 1: 100  Bài lập trình Python có lời giải cơ bản đến nâng cao PDF

Phần 2: 200  Bài lập trình Python có lời giải cơ bản đến nâng cao PDF

Tại sao bạn cần bộ 200 bài tập Python này?

Lập trình là kỹ năng cần sự rèn luyện liên tục. Theo các chuyên gia IT, sai lầm lớn nhất của người mới học là đọc quá nhiều lý thuyết mà thiếu thực hành. Bộ tài liệu PDF này được tổng hợp và chọn lọc kỹ lưỡng nhằm giải quyết các vấn đề sau:

• Phân loại rõ ràng: Bài tập đi từ cấp độ “vỡ lòng” (Level 1) đến các thuật toán phức tạp (Level 3-4).

• Có lời giải chi tiết (Source code): Giúp bạn so sánh, đối chiếu và tối ưu hóa cách viết code của mình.

• Đa dạng chủ đề: Bao quát từ xử lý chuỗi, vòng lặp, đến hướng đối tượng (OOP) và xử lý file.

• Định dạng PDF tiện lợi: Dễ dàng tải về, in ấn hoặc xem offline trên mọi thiết bị.

Nội dung chi tiết trong bộ tài liệu PDF

Bộ tài liệu được chia làm 3 giai đoạn chính, phù hợp với lộ trình phát triển tư duy lập trình:

1. Giai đoạn Cơ bản (Level 1)

Đây là phần khởi động dành cho người mới bắt đầu (newbie). Các bài tập tập trung vào:

• Cú pháp cơ bản của Python.

• Các kiểu dữ liệu: Number, String, List, Tuple, Dictionary.

• Cấu trúc điều khiển: If-Else, Vòng lặp For/While.

• Nhập xuất dữ liệu cơ bản.

2. Giai đoạn Trung cấp (Level 2)

Sau khi đã quen tay, bạn sẽ bước vào các bài toán yêu cầu tư duy logic cao hơn:

• Xây dựng và sử dụng Hàm (Function).

• Các module toán học (Math, Random).

• Xử lý chuỗi nâng cao và Biểu thức chính quy (Regex).

• Thao tác với mảng đa chiều.

3. Giai đoạn Nâng cao (Level 3 & Level 4)

Phần này dành cho những bạn muốn tối ưu code và hiểu sâu về Python:

• Lập trình hướng đối tượng (Class, Object, Inheritance).

• Thuật toán sắp xếp và tìm kiếm.

• Xử lý File (Đọc/Ghi file text, csv, json).

• Xử lý ngoại lệ (Try/Except).

Lưu ý: Tất cả các bài tập đều đi kèm lời giải mẫu (solution) để bạn tham khảo sau khi tự giải.

Bài 0101. In hình tam giác vuông cân bằng dấu *?

h=int(input())
for i in range(1,h+1):
    print(i*'*')

Bài 0102. In hình chữ nhật đặc bằng dấu *?

a,b=map(int,input().split())
for i in range(b):
    print(a*'*')

Bài 0103. In tam giác số?

a=int(input())
b=[]
for i in range(1,a+1):
    b.append(i)
for i in range(1,len(b)+1):
    print(*b[:i])

Bài 0104. In ra bảng cửu chương của số tự nhiên n theo định dạng phép nhân?

n=int(input())
for i in range(1,10):
    print(i,'x',n,'=',n*i)

Bài 0105. Đếm ước của một số nguyên n?

n=int(input())
dem=0
for i in range(1,n+1):
    if n%i==0:
        dem+=1
print(dem)

0106. Kiểm tra n có phải là số nguyên tố (Prime)?

def ktnt(n):
    i=2
    while i*i<=n and n%i!=0:
        i+=1
    return i*i>n and n>1
a=int(input())
if ktnt(a):
    print('Yes')
else:
    print('No')

0107. Kiểm tra một số nguyên có là số hoàn hảo (Perfect)?

def kthh(n):
    tong=0
    for i in range(1,n):# cach 2: nhanh hon range(1, int(n/2)+1) chi chay phan nua
        if n%i==0:
            tong+=i
    return tong
n=int(input())
tong=kthh(n)
if tong==n:
    print('Yes')
else:
    print('No')

0108. Kiểm tra một số nguyên có là số tam giác (Triangular)?

def kttg(n):
    tong=0
    for i in range(1,int(n/2)+1):
        tong+=i
        if tong==n:
            return True
    return False
n=int(input())
if kttg(n):
    print('Yes')
else:
    print('No')

0109. Kiểm tra một số nguyên có là số đối xứng (Palindrome)?

a=input()
if a==a[::-1]:
    print('Yes')
else:
    print('No')

0110. Kiểm tra một số nguyên có là số Chen?

def ktnt(n):
    i=2
    while i*i<=n and n%i!=0:
        i+=1
    return  i*i>n and n>1
a=int(input())
if ktnt(a+2) and ktnt(a):
    print('Yes')
else:
    print('No')

0111. Kiểm tra một số nguyên có là số kỳ ảo (Magic)?

def so_magic(s):
    for i in range(1,len(s)+1):
        sub=int(s[:i])
        if sub%i!=0:
            return False
    return True
s=input()
if so_magic(s):
    print('Yes')
else:
    print('No')

Nguồn : https://xn--300bicode-t1a.vn/

Tác Giả: Trần Phí An Bình

Tải xuống tài liệu PDF (Full Source Code)

Đừng để việc học lập trình dừng lại ở lý thuyết. Hãy tải ngay bộ tài liệu này và bắt đầu “code” ngay hôm nay!

[ [DOWNLOAD] 200 BÀI LẬP TRÌNH PYTHON CÓ LỜI GIẢI (PDF) ]

Hướng dẫn sử dụng:

1. Tải file về máy.

2. Mở đề bài và tự làm trước.

3. Nếu bí hoặc gặp lỗi, hãy tham khảo phần lời giải (solution) đi kèm.

4. Cố gắng tối ưu code ngắn gọn hơn cả lời giải mẫu.

Chúc các bạn học tốt và sớm trở thành một Python Developer chuyên nghiệp!

Câu hỏi thường gặp về bộ 200 bài tập Python (FAQ)

1. Tài liệu này có phù hợp cho người mới bắt đầu (newbie) không?

Hoàn toàn phù hợp. Bộ 200 bài tập này được thiết kế theo lộ trình thăng tiến rõ ràng, đi từ Level 1 (Cơ bản) đến Level 4 (Nâng cao). Người mới bắt đầu có thể làm quen từ các bài toán nhập xuất dữ liệu, câu lệnh điều kiện đơn giản trước khi chuyển sang các thuật toán phức tạp hơn ở phần sau.

2. Tôi có thể xem lời giải chi tiết ở đâu?

Mỗi bài tập trong file PDF đều đi kèm với Source Code (mã nguồn) lời giải mẫu ở ngay bên dưới đề bài. Để đạt hiệu quả tốt nhất, bạn nên tự mình giải bài toán trước, sau đó mới đối chiếu với đáp án để học cách tối ưu logic và cú pháp.

3. Tải bộ tài liệu PDF này có mất phí không?

Không, bộ tài liệu “200 Bài lập trình Python có lời giải” này được chia sẻ hoàn toàn miễn phí nhằm hỗ trợ cộng đồng học lập trình tại Việt Nam. Bạn có thể thoải mái tải về, lưu trữ trên máy tính hoặc in ra giấy để tiện ôn tập.

4. Tôi cần cài đặt phần mềm gì để chạy code Python?

Để thực hành các bài tập này, bạn cần cài đặt Python (tải từ python.org). Về công cụ viết code (IDE), bạn có thể dùng IDLE mặc định, hoặc các phần mềm chuyên nghiệp hơn như Visual Studio Code (VS Code) hoặc PyCharm Community để hỗ trợ gợi ý code và gỡ lỗi tốt hơn.

2 Khóa Học Tin Học Online Thầy Dân Luyện Thi Chuyên Tin Tin Văn Phòng Cấp Tốc

Tổng Hợp Các Hàm Python “Cốt Lõi” Khi Thi HSG Tỉnh Và Vào 10 Chuyên Tin ( Mới Nhất – Chọn Lọc – Cập Nhật Thường Xuyên )

• Cập nhật mới nhất ngày 11/4 /2026
• Trong các kỳ thi học sinh giỏi Tin học cấp huyện – cấp tỉnh và thi tuyển sinh vào lớp 10 chuyên Tin, Python là ngôn ngữ được sử dụng rất phổ biến. Tuy nhiên, đề thi không yêu cầu viết code dài, mà yêu cầu:

  • Nắm chắc hàm chuẩn

  • Biết áp dụng nhanh đúng chỗ

  • Tối ưu tư duy + thời gian làm bài

Tải về ngay tài liệu Tổng Hợp Hàm Python Thi Tỉnh Và Thi Vào Lớp 10 Chuyên Tin

• Bài viết này tổng hợp đầy đủ các hàm Python “xương sống” thường xuất hiện trong đề thi tỉnh và đề thi chuyên, được chia theo nhóm bài toán, kèm ví dụ sát đề thật.
• Tác giả: [Thầy Tấn Dân]
• Chuyên mục: Lập trình thi đấu Python cấp Tỉnh, Ôn thi Chuyên Tin.
• Trong những năm gần đây, Python đã trở thành ngôn ngữ được cho phép và ưa chuộng trong các kỳ thi Học sinh giỏi (HSG) cấp Tỉnh và thi vào lớp 10 Chuyên Tin nhờ cú pháp ngắn gọn. Tuy nhiên, tốc độ thực thi của Python chậm hơn C++. Để bù đắp điều này, việc nắm vững các hàm có sẵn (built-in functions) và các thư viện chuẩn là chìa khóa để code nhanh hơn và tối ưu thời gian chạy (Time Limit).
• Bài viết này sẽ tổng hợp “kho vũ khí” các hàm Python quan trọng nhất giúp bạn chinh phục các bài toán xử lý chuỗi, số học và cấu trúc dữ liệu.

1. Tăng Tốc Nhập/Xuất Dữ Liệu (Fast I/O)

Trong các bài thi, dữ liệu đầu vào có thể lên tới $10^5$ hoặc $10^6$ dòng. Hàm input() thông thường có thể khiến bạn bị lỗi TLE (Time Limit Exceeded).

Hãy sử dụng sys.stdin:

import sys

# Thay thế input() bằng sys.stdin.readline
input = sys.stdin.readline

# Đọc mảng số nguyên trên một dòng
a = list(map(int, input().split()))

Lưu ý: Khi dùng sys.stdin.readline, chuỗi nhận được sẽ kèm theo ký tự xuống dòng \n. Bạn có thể cần dùng .strip() để loại bỏ nó.

2. Các Hàm Xử Lý Chuỗi (String Manipulation)

Đề thi cấp Tỉnh và vào 10 thường xuyên có bài tập xử lý xâu. Python là “vua” ở mảng này.

Cắt và Gộp Chuỗi

• s.split(): Tách chuỗi thành list (mặc định tách theo khoảng trắng).

• " ".join(list): Gộp list thành chuỗi.

Tìm Kiếm và Thay Thế

• s.find(sub): Trả về chỉ số đầu tiên tìm thấy, nếu không có trả về -1.

• s.count(sub): Đếm số lần xuất hiện của chuỗi con.

• s.replace(old, new): Thay thế chuỗi con.

Kỹ Thuật Slicing (Cắt lát)

Đây là kỹ thuật cực mạnh của Python:

• s[::-1]: Đảo ngược chuỗi (Cực hay dùng để kiểm tra số Palindrome).

• s[start:end:step]: Cắt chuỗi linh hoạt.

3. Thư Viện Toán Học (math)

Đừng tự viết hàm tính toán nếu Python đã có sẵn, vì hàm của thư viện C-based chạy nhanh hơn nhiều.

import math

• math.gcd(a, b): Tìm ước chung lớn nhất (UCLN).

• math.lcm(a, b): Tìm bội chung nhỏ nhất (BCNN) (Lưu ý: Chỉ có từ Python 3.9 trở lên).

• math.isqrt(n): Tính căn bậc 2 nguyên (trả về phần nguyên), nhanh và chính xác hơn int(math.sqrt(n)) với số lớn.

• math.ceil(x) / math.floor(x): Làm tròn lên / xuống.

• math.factorial(n): Tính giai thừa $n!$.

4. Xử Lý Danh Sách (List) & Sắp Xếp

Sắp xếp (Sorting) là bài toán kinh điển. Python sử dụng thuật toán Timsort với độ phức tạp $O(N \log N)$.

Hàm Sắp Xếp

• a.sort(): Sắp xếp trực tiếp trên list a (làm thay đổi a).

• sorted(a): Trả về một list mới đã sắp xếp, giữ nguyên a.

• Sắp xếp ngược: Thêm tham số reverse=True.

Sắp Xếp Tùy Chọn (Lambda)

Ví dụ: Sắp xếp các cặp số (x, y) theo y tăng dần:

points = [(1, 3), (4, 1), (2, 2)]
points.sort(key=lambda x: x[1])
# Kết quả: [(4, 1), (2, 2), (1, 3)]

List Comprehension (Tạo List nhanh)

Thay vì dùng vòng lặp for, hãy dùng cách này để code ngắn gọn:

# Tạo mảng bình phương các số chẵn từ 0 đến 9
sq = [x**2 for x in range(10) if x % 2 == 0]

5. “Vũ Khí Bí Mật”: Thư Viện collections và itertools

Đây là phần phân loại thí sinh. Biết dùng các thư viện này sẽ giúp bạn giải quyết bài toán phức tạp trong vài dòng code.

collections.Counter (Đếm tần suất)

Giải quyết bài toán “đếm số lần xuất hiện của phần tử” trong $O(N)$.

from collections import Counter

a = [1, 2, 2, 3, 1, 1]
dem = Counter(a)
print(dem[1]) # Kết quả: 3 (số 1 xuất hiện 3 lần)
print(dem.most_common(1)) # Trả về phần tử xuất hiện nhiều nhất

collections.deque (Hàng đợi hai đầu)

Dùng cho thuật toán BFS hoặc các bài toán cần thêm/xóa phần tử ở đầu mảng (List thường xóa đầu mất $O(N)$, deque chỉ mất $O(1)$).

itertools.permutations & combinations

Dùng để sinh hoán vị và tổ hợp (thay thế cho quay lui – backtracking ở các bài toán có N nhỏ).

from itertools import permutations
# Sinh tất cả hoán vị của [1, 2, 3]
perms = list(permutations([1, 2, 3]))

6. Mẹo Nhỏ Nhưng “Có Võ”

1. Nới rộng giới hạn đệ quy: Python mặc định giới hạn độ sâu đệ quy khoảng 1000. Với các bài DFS hoặc quy hoạch động đệ quy, hãy thêm dòng này đầu file:

   Python

   import sys
   sys.setrecursionlimit(10**6)
   

2. Sử dụng hàm set(): Để loại bỏ phần tử trùng lặp hoặc kiểm tra sự tồn tại trong $O(1)$ thay vì $O(N)$ của list.

3. Hàm zip(): Duyệt song song nhiều list cùng lúc.

I. Các hàm đặc biệt quan trọng – Hay ra nhất trong đề thi

1) các hàm chữ:

1. s=s.split() #tách các chữ mất khoản cách
2. s=s.split(‘,’) # tách các phần tử bởi dấu phẩy (, ) (.) (: ) tùy bài
3. isdigit() # các số 
4. islower() ( chữ thường )
5. isupper() (chữ hoa )
6. sorted() ( Các từ theo thứ tự từ điển)
7. print(s1.count(s2)) ( điếm trong chuỗi )
8. s[i].isalnum() lấy kiểu chữ và số ( trừ ký tự đặc biệt )
9. not s[i].isalnum() lấy ký tự đặc biệt
10. s=’’.join(a)# chuyển mảng sang chuỗi
11. a=list(s) # chuyển chuỗi sang mảng
12. vt=c.index(Max)
13. vt=s.rfind(‘.’)# tìm vị trí dấu chấm cuối
14. vt=s.find(‘.’)# tìm vị trí đầu trong chuỗi
15. abs( a- b) ( hàm trị tuyệt đối)
16. sqrt ( a) căn bật 2 nhớ import math
17. BCNN=abs(a*b)/ucln(a,b) # Bội số chung lớn nhất
18. Ucln=math.gcd(a,b) #Ước số chung lớn nhất

print(s[0].zfill(2),’:’,s[1].zfill(2),’:’,s[2].zfill(2),sep=”)# định dạng thêm số 0 ở phía trước zfill(2) ; số 2 phần chục; 3; phần trăm; 4; phần ngàn,…

7. Kỹ Thuật Lọc Dữ Liệu Bằng “Biểu Thức Chính Quy” (Regex)

Trong đề thi, đôi khi dữ liệu vào là một xâu hỗn độn chứa cả chữ và số (ví dụ: a12b34cd56), và yêu cầu bạn tách riêng số hoặc chữ. Thay vì dùng vòng lặp for để kiểm tra từng ký tự, ta dùng thư viện re (Regular Expression).

Lấy từng số, bỏ chữ (Hoặc ngược lại)

Để sử dụng, bắt buộc phải import re.

import re

s = "hoc123sinh456gioi789"

# 1. Lấy số, bỏ chữ:
# '[^0-9]+' nghĩa là: Những ký tự KHÔNG phải số (0-9)
# Thay thế những cái không phải số bằng khoảng trắng ' ', sau đó split ra.
nums = re.sub('[^0-9]+', ' ', s).split()
# Kết quả nums: ['123', '456', '789'] (Dạng chuỗi)

# 2. Lấy chữ, bỏ số:
# '[^a-zA-Z]+' nghĩa là: Những ký tự KHÔNG phải chữ cái (a-z, A-Z)
words = re.sub('[^a-zA-Z]+', ' ', s).split()
# Kết quả words: ['hoc', 'sinh', 'gioi']

Tại sao nó “xịn”? Cách này xử lý được cả trường hợp số âm hoặc số thực nếu bạn chỉnh pattern một chút, và nó nhanh hơn nhiều so với việc viết hàm if kiểm tra từng ký tự.

8. Sửa Đổi và Làm Sạch Chuỗi (replace & strip)

Nhóm hàm này dùng để chuẩn hóa dữ liệu đầu vào (ví dụ: xoá khoảng trắng thừa, thay thế từ khóa).

Hàm thay thế (replace)

Dùng để thay thế tất cả các chuỗi con tìm thấy.

s = "  hello world  "

# Xóa toàn bộ khoảng trắng trong chuỗi
# Kết quả: "helloworld"
clean_s = s.replace(" ", "") 

# Thay thế từ
s2 = "python is hard"
s2 = s2.replace("hard", "easy") 
# Kết quả: "python is easy"

Hàm cắt khoảng trắng (strip)

Rất quan trọng khi đọc dữ liệu từ input() để tránh lỗi do khoảng trắng thừa ở đầu/cuối dòng.

• s.strip(): Cắt khoảng trắng 2 đầu.

• s.lstrip(): Cắt bên trái (đầu dòng).

• s.rstrip(): Cắt bên phải (cuối dòng).

9. Các Kỹ Thuật Sắp Xếp và Đảo Ngược

Cần phân biệt rõ giữa Sắp xếp (Sort) và Đảo ngược (Reverse).

Sắp xếp (Sort)

Đưa các phần tử về trật tự tăng dần hoặc giảm dần.

a = [3, 1, 5, 2]

# Cách 1: a.sort()
# Sắp xếp trực tiếp lên biến a. Không trả về dữ liệu mới.
a.sort() 
print(a) # [1, 2, 3, 5]

# Cách 2: sorted(a)
# Trả về một list MỚI, list a cũ giữ nguyên.
b = sorted(a, reverse=True) # Sắp xếp giảm dần
print(b) # [5, 3, 2, 1]

Đảo ngược (Reverse – Slicing)

Đây không phải là sắp xếp lại giá trị, mà chỉ là lật ngược vị trí (đuôi lên đầu).

s = "ABCDE"
rev_s = s[::-1] 
# Kết quả: "EDCBA"

Kiểm tra đối xứng (Palindrome)

Sử dụng kỹ thuật slicing [::-1] để kiểm tra cực nhanh.

def ktdx(n):
    # Luôn chuyển về chuỗi trước khi đảo ngược
    s = str(n) 
    return s == s[::-1]

print(ktdx(12321)) # True
print(ktdx(123))   # False

10. Tìm Giá Trị Lớn Nhất / Nhỏ Nhất (Min/Max Nâng Cao)

Ngoài việc tìm số lớn nhất/nhỏ nhất thông thường, Python cho phép tìm theo tiêu chí riêng bằng tham số key.

Min/Max cơ bản

arr = [10, 5, 8, 90]
print(max(arr)) # 90
print(min(arr)) # 5

Min/Max theo độ dài (Rất hay thi)

Ví dụ: Tìm từ dài nhất trong một câu.

words = ["ha", "noi", "vietnam", "yeu"]

# Tìm chuỗi có độ dài (len) lớn nhất
longest = max(words, key=len)
print(longest) # "vietnam"

# Tìm chuỗi có độ dài nhỏ nhất
shortest = min(words, key=len)
print(shortest) # "ha"

Giải thích: key=len bảo Python rằng: “Đừng so sánh chữ cái a,b,c… hãy so sánh độ dài của chúng để quyết định ai lớn nhất”.

Tổng kết nhanh các hàm cần nhớ:

9) lấy điểm ra sắp xếp:

Def laydiem(s):

          s=s.split()

          return float(s[-1])

kq=sorted(a,key=laydiemm,reverse=True)

for i in range(len(kq)):

          x=kq[i].split()

          diem=float(x[-1])

          x.pop(-1)

          hoten=’’.join(x)

          print(hoten,’%0.1f’%diem)

2 Khóa Học Tin Học Online Thầy Dân Luyện Thi Chuyên Tin Tin Văn Phòng Cấp Tốc

Nếu bạn đang ôn thi học sinh giỏi Tin học THCS cấp tỉnh Tiền Giang, đặc biệt là thi lập trình Python, thì bài viết này sinh ra là dành cho bạn.

Trong bài này, Vi Tính Tân Dân đã tổng hợp 73 đề thi HSG Tin học Python THCS cấp tỉnh Tiền Giang, kèm đáp án – code giải chi tiết – giải thích thuật toán rõ ràng, bám sát đúng cấu trúc đề thi thực tế của Sở GD&ĐT Tiền Giang.

👉 Phù hợp cho:

• Học sinh lớp 6 – 9 ôn thi HSG Tin học

• Học sinh luyện thi vào lớp 10 chuyên Tin

• Giáo viên, phụ huynh bồi dưỡng học sinh năng khiếu Tin học

🎯 Vì sao nên luyện bộ 73 đề thi HSG Tin học Python THCS cấp tỉnh Tiền Giang này?

Không giống các bộ đề tràn lan trên mạng, bộ đề này được chọn lọc kỹ, đảm bảo:

✅ Đúng chuẩn đề thi Tin học THCS cấp tỉnh Tiền Giang
✅ Ngôn ngữ Python – đúng yêu cầu thi thực tế
✅ Có đáp án + code mẫu
✅ Giải thích tư duy thuật toán, không chỉ cho code
✅ Từ dễ → trung bình → khó, giúp nâng trình rõ rệt

👉 Rất nhiều học sinh học Python nhưng không biết ra đề thi thật trông như thế nào. Bộ đề này giúp bạn làm quen đề chuẩn – tránh bỡ ngỡ khi đi thi.

📚 Nội dung chính trong 73 đề thi HSG Tin học Python THCS

Bộ đề bao phủ toàn bộ kiến thức trọng tâm thường ra trong các kỳ thi HSG Tin học cấp tỉnh:

🔹 1. Xử lý số & toán học trong Python

• 1. Đọc số nguyên x từ file NUM.INP.
  2. Duyệt hai số a và b trong phạm vi [1, x], đảm bảo a ≤ b.
  3. Kiểm tra điều kiện a * b == x và a / b ≥ 0.5.
  4. Nếu tìm thấy cặp (a, b) thỏa mãn, gán la_ket_doi = 1 và dừng vòng lặp.
  5. Ghi kết quả 1 vào NUM.OUT nếu x là số kết đôi, ngược lại ghi 0.

🔹 2. Xử lý ngày tháng năm

• 1. Đọc dữ liệu từ file CUP.INP, bao gồm:
     • Ngày hiện tại (định dạng dd.mm.yyyy).
     • Số ngày cần cộng thêm.
  2. Chuyển đổi ngày hiện tại thành kiểu datetime.
  3. Cộng thêm số ngày vào ngày hiện tại bằng timedelta(days=so_ngay_them).
  4. Xuất kết quả với định dạng dd.mm.yyyy ra file CUP.OUT.

🔹 3. Chuỗi ký tự (String)

• 1. Đọc dữ liệu từ file PART.INP, gồm:
     • n, L, R: số phần tử của mảng và khoảng cần kiểm tra.
     • Mảng a chứa n số nguyên.
  2. Duyệt qua từng phần tử a[i] của mảng:
     • Xét các chỉ số j trong phạm vi [i+L, i+R].
     • Nếu a[i] == a[j] + a[j-1], tăng biến đếm và dừng kiểm tra tiếp theo.
  3. Xuất kết quả ra file PART.OUT.

🔹 4. Xử lý Xâu

• Đọc dữ liệu từ file PW.INP:
  • Số nguyên n là số xâu.
  • n xâu ký tự chứa chỉ các chữ cái thường (a-z).

    Sắp xếp các xâu theo độ dài tăng dần.

    Duyệt từng xâu trong danh sách:

  • Kiểm tra xem xâu đó có chứa tất cả các xâu khác hay không.
  • Nếu có, in ra xâu đó và dừng lại.

    Nếu không có xâu nào phù hợp, in -1.

🔹 5. Thuật toán cơ bản – nâng cao

• 1. Đọc dữ liệu từ COVID.INP:
     • n: số người trên đường.
     • a: danh sách tọa độ của n người.
  2. Sắp xếp danh sách tọa độ theo thứ tự tăng dần.
  3. Tính toán khoảng cách giữa các vị trí:
     • Khoảng cách nhỏ nhất giữa hai người gần nhau nhất.
     • Khoảng cách lớn nhất giữa người đầu và người cuối.
  4. Tính số nhóm nhiễm bệnh dựa trên khoảng cách:
     • Tối thiểu: nếu khoảng cách nhỏ nhất là d, thì nhóm nhiễm bệnh sẽ là (d // 2) + 1.
     • Tối đa: nếu khoảng cách lớn nhất là D, thì nhóm nhiễm bệnh sẽ là (D // 2) + 1.
  5. In kết quả.

🧠 Có gì trong phần ĐÁP ÁN & CODE GIẢI?

Điểm mạnh nhất của bộ tài liệu này là không chỉ có đáp án, mà còn:

✔️ Code Python rõ ràng – đúng chuẩn thi
✔️ Có import sys, đọc ghi file đúng format đề tỉnh
✔️ Giải thích từng bước tư duy
✔️ Phân tích độ phức tạp thuật toán
✔️ Chú thích bằng tiếng Việt dễ hiểu cho học sinh THCS

👉 Phù hợp cả với:

• Học sinh tự học tại nhà

• Giáo viên soạn tài liệu bồi dưỡng

• Phụ huynh theo dõi quá trình học của con

🏆 Lợi ích khi luyện trọn bộ 73 đề này

📌 Nắm chắc cấu trúc đề thi HSG Tin học tỉnh Tiền Giang
📌 Tăng khả năng tư duy thuật toán – không học vẹt
📌 Làm quen cách trình bày code đúng chuẩn chấm thi
📌 Tự tin khi bước vào kỳ thi chính thức
📌 Rút ngắn rất nhiều thời gian ôn tập

👉 Rất nhiều học sinh từng đạt giải cấp huyện – cấp tỉnh đã luyện theo đúng dạng đề như trong bộ này.

👨‍🏫 Ai nên sử dụng bộ đề này?

✔️ Học sinh THCS yêu thích Tin học
✔️ Học sinh đang học Python để thi HSG
✔️ Học sinh ôn thi vào lớp 10 chuyên Tin
✔️ Giáo viên Tin học THCS
✔️ Trung tâm bồi dưỡng học sinh giỏi Tin học

🚀 Kết luận

Bộ 73 Đề thi HSG Tin học Python THCS cấp tỉnh Tiền Giang có ĐÁP ÁN là tài liệu cực kỳ giá trị nếu bạn đang nghiêm túc theo đuổi con đường học sinh giỏi Tin học.

👉 Nếu bạn muốn:

• Học đúng trọng tâm

• Luyện đúng dạng đề

• Hiểu bản chất thuật toán

👉 Đừng bỏ qua bộ đề này.

📌 Theo dõi vitinhtandan.com để cập nhật thêm:

• Đề thi HSG Tin học mới

• Code Python giải chi tiết

• Tài liệu ôn thi chuyên Tin từ cơ bản đến nâng cao

ĐÁP ÁN CÂU 1: Số Kết Đôi

import sys

sys.stdin = open("NUM.INP", "r")
sys.stdout = open("NUM.OUT", "w")

# Doc so x
x = int(sys.stdin.readline().strip())

# Kiem tra so ket doi
la_ket_doi = 0
for a in range(1, x + 1):
    for b in range(a, x + 1):
        if a * b == x and a / b >= 0.5:
            la_ket_doi = 1
            break
    if la_ket_doi:
        break

# Ghi ket qua
print(la_ket_doi)

1️⃣ Ý tưởng thuật toán

Ta cần kiểm tra số nguyên dương x có tồn tại hai số nguyên dương a, b sao cho:

• a×b=x

• a≤b

• a/b≥0.5

Nếu tồn tại ít nhất một cặp (a, b) thỏa mãn thì x là số kết đôi → in 1, ngược lại in 0.

2️⃣ Phân tích từng bước chương trình

🔹 Bước 1: Đọc dữ liệu

Đọc số nguyên dương x từ file NUM.INP.

🔹 Bước 2: Duyệt các cặp (a, b)

• a chạy từ 1 đến x

• b chạy từ a đến x → đảm bảo a ≤ b, tránh xét trùng cặp

🔹 Bước 3: Kiểm tra điều kiện số kết đôi

• a * b == x → (a, b) là một cặp ước của x

• a / b ≥ 0.5 → đúng điều kiện đề bài

👉 Nếu thỏa mãn:

• Gán la_ket_doi = 1

• Dừng vòng lặp ngay (không cần xét thêm)

🔹 Bước 4: Xuất kết quả

• In 1 nếu x là số kết đôi

• In 0 nếu không tồn tại cặp nào thỏa

3️⃣ Độ phức tạp thuật toán

⏱️ Thời gian chạy

• Vòng a: chạy tối đa x lần

• Với mỗi a, vòng b: chạy tối đa x − a + 1 lần

👉 Trường hợp xấu nhất:

O(x^2)

💾 Bộ nhớ sử dụng

• Chỉ dùng vài biến đơn giản (x, a, b, la_ket_doi)

• Không dùng mảng hay cấu trúc phức tạp

👉 Độ phức tạp bộ nhớ:

O(1)

4️⃣ Nhận xét theo góc nhìn bài thi

✔️ Thuật toán:

• Dễ hiểu

• Dễ cài đặt

• Phù hợp mức THCS – HSG cấp huyện/tỉnh

⚠️ Nhược điểm:

• Với x lớn → chạy chậm do O(x²)

👉 Trong bài thi nâng cao, có thể tối ưu bằng cách chỉ duyệt đến √x, nhưng đáp án này hoàn toàn hợp lệ nếu đề không yêu cầu tối ưu.

ĐÁP ÁN CÂU 2: Word Cup

import sys
from datetime import datetime, timedelta

sys.stdin = open("CUP.INP", "r")
sys.stdout = open("CUP.OUT", "w")

# Doc du lieu
ngay_hien_tai = sys.stdin.readline().strip()
so_ngay_them = int(sys.stdin.readline().strip())

# Chuyen doi ngay thanh doi tuong datetime
ngay_hien_tai = datetime.strptime(ngay_hien_tai, "%d.%m.%Y")

# Cong them so ngay
ngay_tuong_lai = ngay_hien_tai + timedelta(days=so_ngay_them)

# In ket qua theo dinh dang dd.mm.yyyy
print(ngay_tuong_lai.strftime("%d.%m.%Y"))

1️⃣ Ý tưởng thuật toán

Bài toán yêu cầu:

• Cho một ngày hiện tại (định dạng dd.mm.yyyy)

• Cho số ngày cần cộng thêm

• Tính và in ra ngày tương lai sau khi cộng số ngày đó

👉 Đây là bài toán xử lý ngày tháng, cần xét đúng:

• Tháng có 28, 29, 30 hay 31 ngày

• Năm nhuận