74 Đề thi học sinh giỏi Tin học THCS cấp Tỉnh Có ĐÁP ÁN 2026-2027
Tổng Hợp 74 Đề Thi Học Sinh Giỏi Tin Học THCS Cấp Tỉnh Có Đáp Án (Năm Học 2026-2027)
Kỳ thi chọn học sinh giỏi Tin học cấp THCS (đặc biệt là lớp 9) luôn là một thử thách lớn đòi hỏi sự chuẩn bị kỹ lưỡng về tư duy thuật toán và kỹ năng lập trình. Để đồng hành cùng các thầy cô giáo và các em học sinh, Vi Tính Tấn Dân xin chia sẻ bộ tài liệu “74 Đề thi học sinh giỏi Tin học THCS cấp tỉnh có đáp án” được cập nhật mới nhất cho năm học 2026-2027.
Đây là nguồn tài liệu quý giá giúp các em làm quen với cấu trúc đề thi, rèn luyện kỹ năng giải thuật trên các ngôn ngữ phổ biến như C++, Python và Pascal.
Các đề ôn thi để chuẩn bị thi Cấp Xã thì các em vào đường dẫn phía dưới để tham khảo giúp thầy nhé!
- Giải đề 1 và đáp án thi Học sinh giỏi tin học Python C++ THCS có tài liệu ôn thi
- Giải đề 2 và đáp án thi Học sinh giỏi tin học Python C++ THCS có tài liệu ôn thi
- Giải đề 3 thi học sinh giỏi tin học lập trình Python có đáp án
- Giải đề 4 ôn thi học sinh giỏi Tin Học THCS lập trình Python có đáp án
- Giải đề 5 và đáp án thi HSG Tin Python có số Pell.
- Giải đề 6 và đáp án bồi dưỡng học sinh giỏi tin 10 có số Armstrong
- Giải đề 7 và đáp án thi học sinh giỏi tin học 10 Python có số Collatz
- Giải đề 8 trong 20 đề Bồi dưỡng học sinh giỏi Tin học lớp 9 có số Kaprekar.
- Giải đề 9 thi HSG Tin học lớp 8 lập trình Python có số Happy
- Giải đề 10 thi tin học trẻ THPT có bài In các xâu con trong xâu s.
- Đề thi hsg tin 11 python có đáp án hay nhất 2024
- 12 đề và đáp án thi HSG tin Python có sắp xếp
- Đề 13 thi học sinh giỏi Tin học THCS có đáp án hay nhất năm 2024.
- 14 đề bồi dưỡng học sinh giỏi tin học lớp 7, 8, 9 THCS mới nhất !
- 15 Đề thi học sinh giỏi Tin học lớp 9 cấp huyện hay nhất 2024 – 2025
- 16 Đề bài tập Python có lời giải PDF thi HSG cấp huyện mới nhất
- 17 đề thi tin học trẻ có Đáp Án python THCS cấp huyện PDF
- 18 Đề thi học sinh giỏi Tin học THCS có đáp ÁN dễ học nhất năm 2025
- 19 thi HSG Tin 9 C ++ hoặc Python có đáp án
- 100 đề và đáp án thi HSG tin Python cấp huyện 2025
1. Tại sao bạn nên tải bộ 74 đề thi HSG Tin học này?
Khác với các tài liệu trôi nổi trên mạng, bộ sưu tập 74 đề thi này được Vi Tính Tấn Dân tổng hợp và chọn lọc kỹ càng từ các kỳ thi chính thức của nhiều tỉnh thành trên cả nước trong những năm gần đây.
Số lượng lớn: Với 74 đề thi, học sinh có thể thoả sức luyện tập từ cơ bản đến nâng cao.
Có đáp án chi tiết: Tất cả các đề đều đi kèm Test case (Input/Output) chuẩn và Code mẫu (Solution) giúp học sinh dễ dàng đối chiếu kết quả.
Cập nhật xu hướng mới: Đề thi bám sát cấu trúc ra đề của Bộ GD&ĐT và các Sở GD&ĐT trong giai đoạn 2025-2027, tập trung mạnh vào tư duy thuật toán thay vì chỉ cú pháp ngôn ngữ.
2. Cấu trúc đề thi học sinh giỏi Tin học THCS năm 2026-2027 có gì mới?
Theo xu hướng chuyển đổi số và đổi mới giáo dục, đề thi HSG Tin học cấp tỉnh hiện nay thường có cấu trúc như sau:
Thời gian làm bài: 150 phút.
Hình thức: Thi lập trình trên máy tính (chấm tự động bằng các phần mềm như Themis, CMS…).
Ngôn ngữ lập trình: Cho phép sử dụng C++ (phổ biến nhất), Python (xu hướng mới) và Free Pascal.
Các dạng bài tập thường gặp:
Bài toán số học: Tìm số nguyên tố, ước số, số hoàn hảo, xử lý số lớn…
Xử lý mảng và chuỗi: Sắp xếp, tìm kiếm, thao tác trên xâu ký tự.
Thuật toán & Quy hoạch động: Các bài toán tối ưu, bài toán cái túi, dãy con tăng dài nhất…
Hình học & Tổ hợp: Tính diện tích, đếm số phương án…
3. Review nội dung bộ đề thi
Dưới đây là tóm tắt nội dung của một số đề thi tiêu biểu có trong bộ tài liệu này:
Đề số 01: Đề thi HSG Tin học Tỉnh Tiền Giang (Năm 2021- 2022)
Bài 1 (4 điểm): Tìm số nguyên tố đầy đủ?
Bài 2 (4 điểm): Tìm Mật Mã (Mảng 1 chiều + Thuật toán đếm)?
Bài 3 (4 điểm): Bài toán Ma Trận?
Bài 4 (4 điểm): Về hình học Tính Tam Giác?
- Bài 5 (4 điểm): Tính Lãi Kép Ngân Hàng?
(Tất cả đều có code giải tham khảo bằng C++ và Python)
4. Hướng dẫn ôn thi hiệu quả với bộ tài liệu này
Để đạt kết quả cao nhất trong kỳ thi cấp tỉnh, các em học sinh nên tuân thủ lộ trình sau:
Giai đoạn 1: Tải bộ đề về và phân loại theo độ khó.
Giai đoạn 2: Tự bấm giờ làm bài giống như thi thật (không xem đáp án trước).
Giai đoạn 3: So sánh kết quả với bộ Test case.
Giai đoạn 4: Tham khảo Code mẫu để học hỏi cách viết code tối ưu, ngắn gọn và “sạch” hơn.
5. Tải xuống 74 Đề thi học sinh giỏi Tin học THCS cấp tỉnh (Full Code)
Các thầy cô và các em học sinh có thể tải trọn bộ tài liệu tại liên kết bên dưới. File nén bao gồm: File đề bài (PDF/Word), Bộ Test (Input/Output), và Code giải (CPP/PY/PAS).
Tải đề Thi Đề thi HSG Tin học THCS Python Cấp Tỉnh file PDF:
Lời kết
Hy vọng bộ tài liệu 74 đề thi học sinh giỏi Tin học THCS cấp tỉnh có đáp án 2026-2027 này sẽ là hành trang vững chắc giúp các em học sinh tự tin bước vào phòng thi và gặt hái giải cao.
Đừng quên ghé thăm Vi Tính Tấn Dân thường xuyên để cập nhật thêm nhiều tài liệu công nghệ, thủ thuật máy tính và đề thi mới nhất nhé!




Đáp Án Bài 1: Số Nguyên Tố Đầy Đủ
import sys
import math
# MỞ FILE VÀO / RA (đúng chuẩn thi)
sys.stdin = open("FULLPRIM.INP", "r")
sys.stdout = open("FULLPRIM.OUT", "w")
# Hàm kiểm tra số nguyên tố
def la_so_nguyen_to(so):
if so < 2:
return False
if so == 2:
return True
if so % 2 == 0:
return False
can_bac_hai = int(math.sqrt(so))
for uoc in range(3, can_bac_hai + 1, 2):
if so % uoc == 0:
return False
return True
# ===== CHƯƠNG TRÌNH CHÍNH =====
# Nhập số lượng phần tử
so_luong = int(input())
# Nhập dãy số
day_so = list(map(int, input().split()))
ket_qua = []
# Duyệt từng số trong dãy
for so in day_so:
if la_so_nguyen_to(so):
so_dao = int(str(so)[::-1])
if la_so_nguyen_to(so_dao):
ket_qua.append(str(so))
# Xuất kết quả
if len(ket_qua) == 0:
print(0)
else:
print(" ".join(ket_qua))🧠 Giải thích ngắn gọn cách làm
Viết hàm
la_so_nguyen_to()để kiểm tra số nguyên tốVới mỗi số trong dãy:
Kiểm tra số đó có nguyên tố không
Đảo ngược số
Kiểm tra số đảo có nguyên tố không
Nếu cả hai đều nguyên tố → là số nguyên tố đẩy đủ
In ra danh sách kết quả, nếu không có in
0
⏱️ Độ phức tạp
Kiểm tra 1 số nguyên tố:
O(√n)Tổng:
Bộ nhớ:
O(1)
Đáp Án Bài 2: Mật Mã:
# SECRCODE.py
import sys
sys.stdin = open("SECRCODE.INP", "r")
sys.stdout = open("SECRCODE.OUT", "w")
xau = sys.stdin.read().strip()
# Mảng đếm số lần xuất hiện của các chữ cái a -> z
dem = [0] * 26
# Đếm ký tự
for ky_tu in xau:
vi_tri = ord(ky_tu) - ord('a')
dem[vi_tri] += 1
# Tạo mã bản quyền
ket_qua = ""
for i in range(26):
if dem[i] > 0:
ket_qua += str(dem[i])
print(ket_qua)
🔹 Phân tích bài toán
Đề bài cho một xâu ký tự thường a–z
Cần:
Đếm số lần xuất hiện của từng chữ cái
Theo thứ tự alphabet a → z
Nếu chữ cái xuất hiện (đếm > 0) thì ghi số lần xuất hiện vào mã
Các số được nối liền nhau, không có dấu cách
🔹 Ví dụ phân tích
Xâu:
| Ký tự | Số lần |
|---|---|
| a | 2 |
| b | 4 |
| c | 6 |
| d | 3 |
| e | 5 |
| f | 1 |
| x | 3 |
| y | 3 |
| z | 4 |
👉 Mã bản quyền: 246351334
🔹 Ý tưởng giải
Dùng mảng đếm 26 phần tử, mỗi phần tử tương ứng một chữ cái
Duyệt xâu:
Mỗi ký tự → tăng biến đếm tương ứng
Duyệt mảng từ
ađếnz:Nếu số đếm > 0 → nối vào kết quả
🔹 Độ phức tạp
Thời gian: O(n) (n là độ dài xâu)
Bộ nhớ: O(1) (chỉ dùng mảng 26 phần tử)
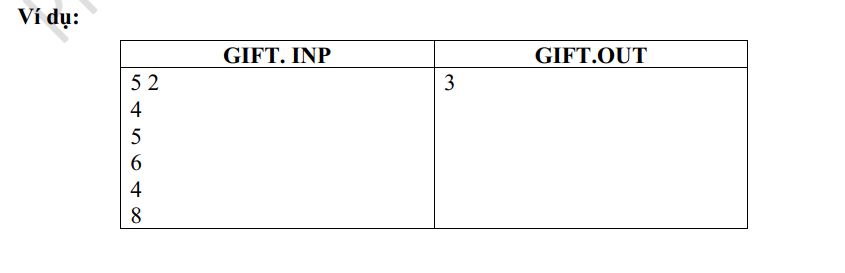
Đáp án bài 3: Chọn Phần Thưởng
# BONUSSEL.py
import sys
import math
sys.stdin = open("BONUSSEL.INP", "r")
sys.stdout = open("BONUSSEL.OUT", "w")
m, n = map(int, sys.stdin.readline().split())
tong = 0
for _ in range(m):
dong = list(map(int, sys.stdin.readline().split()))
for gia_tri in dong:
can = int(math.isqrt(gia_tri))
if can * can == gia_tri:
tong += gia_tri
print(tong)
🔹 Phân tích bài toán
Cho bảng số nguyên dương kích thước m × n
Yêu cầu:
Tìm tất cả các số chính phương
Tính tổng các số đó
🔹 Số chính phương là gì?
Một số x là số chính phương nếu:
👉 Cách kiểm tra nhanh:
🔹 Ý tưởng giải
Đọc m, n
Duyệt từng phần tử trong bảng
Với mỗi số:
Tính căn bậc hai nguyên
Nếu bình phương lại bằng chính nó → cộng vào tổng
🔹 Độ phức tạp
Thời gian: O(m × n)
Bộ nhớ: O(1)
✅ Ghi nhớ khi đi thi
✔ Dùng math.isqrt() chính xác – nhanh – an toàn
✔ Biến đặt rõ nghĩa
✔ Không in thừa dòng, thừa khoảng trắng
Đáp án bài 4: Tam Giác
# TRIANGLE.py
import sys
sys.stdin = open("TRIANGLE.INP", "r")
sys.stdout = open("TRIANGLE.OUT", "w")
def binh_phuong_khoang_cach(x1, y1, x2, y2):
return (x2 - x1) ** 2 + (y2 - y1) ** 2
T = int(sys.stdin.readline())
for _ in range(T):
xa, ya, xb, yb, xc, yc = map(float, sys.stdin.readline().split())
# Kiểm tra 3 điểm có thẳng hàng không
dien_tich = (xb - xa) * (yc - ya) - (xc - xa) * (yb - ya)
if dien_tich == 0:
print("NO")
continue
# Tính bình phương độ dài các cạnh
AB2 = binh_phuong_khoang_cach(xa, ya, xb, yb)
BC2 = binh_phuong_khoang_cach(xb, yb, xc, yc)
CA2 = binh_phuong_khoang_cach(xc, yc, xa, ya)
# Kiểm tra định lý Pitago
if (abs(AB2 + BC2 - CA2) < 1e-9 or
abs(AB2 + CA2 - BC2) < 1e-9 or
abs(BC2 + CA2 - AB2) < 1e-9):
print("YES")
else:
print("NO")
🔹 Phân tích đề bài
Cho T bộ dữ liệu, mỗi bộ gồm tọa độ 3 điểm A, B, C trong mặt phẳng OXY.
Yêu cầu:
👉 Kiểm tra 3 điểm có tạo thành TAM GIÁC VUÔNG hay không
In:
"YES"nếu là tam giác vuông"NO"nếu không phải
🔹 Điều kiện toán học
1️⃣ Ba điểm tạo thành tam giác
Ba điểm không thẳng hàng
⇔ Diện tích tam giác ≠ 0
👉 Kiểm tra bằng tích có hướng:
2️⃣ Tam giác vuông (định lý Pitago)
- Gọi:
AB², BC², CA² là bình phương độ dài các cạnh
- Tam giác vuông nếu:
- ⚠️ KHÔNG lấy căn để tránh sai số số thực (đề đã nhắc)
🔹 Công thức bình phương khoảng cách
Với A(x₁, y₁), B(x₂, y₂):
🔹 Ý tưởng giải
Với mỗi bộ test:
Đọc tọa độ A, B, C
Kiểm tra có tạo thành tam giác
Tính AB², BC², CA²
Kiểm tra định lý Pitago
In kết quả
🔹 Độ phức tạp
Mỗi test: O(1)
Tổng: O(T)
→ Chạy rất nhanh
✅ Giải thích điểm quan trọng (rất hay bị sai)
- ⚠️ KHÔNG dùng
sqrt()
⚠️ So sánh số thực phải dùng sai số nhỏ (1e-9)
⚠️ Phải kiểm tra tạo thành tam giác trước
📌 Mẹo ăn điểm khi thi
- ✔ Dùng bình phương độ dài
✔ So sánh bằngabs(a-b) < 1e-9
✔ In đúng"YES"/"NO"(IN HOA)
1. Bản chất của đoạn code
Đoạn code này dùng để kiểm tra xem một tam giác có phải là tam giác vuông hay không dựa trên Định lý Pitago đảo.
Định lý: Nếu tổng bình phương hai cạnh bằng bình phương cạnh còn lại ($a^2 + b^2 = c^2$) thì đó là tam giác vuông.
Vì chúng ta không biết cạnh nào là cạnh huyền, nên phải kiểm tra cả 3 trường hợp:
AB^2 + BC^2 = CA^2 (Vuông tại B)
AB^2 + CA^2 = BC^2 (Vuông tại A)
BC^2 + CA^2 = AB^2 (Vuông tại C)
2. Tại sao phải dùng abs(...) < 1e-9 mà không dùng dấu ==?
Đây là kiến thức “sống còn” cho học sinh khi thi HSG Tin học.
Vấn đề sai số: Trong máy tính, các số thực (kiểu
float) được lưu dưới dạng nhị phân nên thường xảy ra sai số nhỏ.Ví dụ: Kết quả lẽ ra là
25.0nhưng máy tính có thể lưu là24.99999999999999.Nếu ta dùng
if AB2 + BC2 == CA2:, máy sẽ trả vềFalse(Sai), dẫn đến mất điểm oan.
Giải pháp: Thay vì so sánh bằng nhau tuyệt đối, ta kiểm tra xem hiệu của hai vế có đủ nhỏ hay không.
abs(AB2 + BC2 - CA2)là trị tuyệt đối của hiệu hai vế.1e-9(tức là 10^{-9} hay 0.000000001) được gọi là sai số cho phép (epsilon).
Kết luận: Nếu hiệu của hai vế nhỏ hơn 10^{-9}, ta coi như chúng bằng nhau.
3. Cách giải thích cho học sinh (Ngôn ngữ của Thầy Dân)
Thầy có thể dạy các em như thế này:
Bước 1: Tính bình phương độ dài 3 cạnh (gọi là
AB2,BC2,CA2).Bước 2: Áp dụng Pitago đảo. Nhưng nhớ là trong lập trình, “bằng nhau” với số thực rất mong manh.
Bước 3: Sử dụng “khoảng cách an toàn”. Nếu hai vế chỉ lệch nhau một tí xíu không đáng kể (
< 1e-9) thì máy tính chấp nhận đó là tam giác vuông.
4. Code viết lại cho chuyên nghiệp
Các em có thể đưa đoạn này vào chuyên đề Hình học:
# Giả sử đã tính xong bình phương các cạnh AB2, BC2, CA2
sai_so = 1e-9 # Epsilon
# Kiểm tra từng trường hợp vuông tại A, B, hoặc C
vuong_tai_B = abs(AB2 + BC2 - CA2) < sai_so
vuong_tai_A = abs(AB2 + CA2 - BC2) < sai_so
vuong_tai_C = abs(BC2 + CA2 - AB2) < sai_so
if vuong_tai_A or vuong_tai_B or vuong_tai_C:
print("YES") # Là tam giác vuông
else:
print("NO")Đáp án bài 5: Lãi Kép Ngân Hàng:
# COMPINT.py
import sys
sys.stdin = open("COMPINT.INP", "r")
sys.stdout = open("COMPINT.OUT", "w")
T = int(sys.stdin.readline())
for _ in range(T):
M, r, n = map(float, sys.stdin.readline().split())
n = int(n)
tong_tien = M
# Tính lãi kép qua từng tháng
for _ in range(n):
tong_tien = tong_tien + tong_tien * r / 100
# In kết quả với 1 chữ số thập phân
print(f"{tong_tien:.1f}")
🔹 Phân tích đề bài
Có T khoản gửi tiết kiệm
Mỗi khoản gồm:
M: tiền vốn ban đầur: lãi suất % mỗi thángn: số tháng gửi
Hình thức: LÃI KÉP
Tiền lãi của tháng trước được cộng vào vốn để tính lãi cho tháng sau
👉 Yêu cầu:
Tính tổng số tiền nhận được sau n tháng, in ra 1 chữ số thập phân
🔹 Công thức lãi kép theo tháng
Sau mỗi tháng:
Tương đương:
Lặp lại n lần
🔹 Ví dụ phân tích (đề bài)
Gửi:
Tháng 1:
T1 = 1000000 * 1.007 = 1007000Tháng 2:
T2 = 1007000 * 1.007 = 1014049Tháng 3:
T3 = 1014049 * 1.007 = 1021147.3
🔹 Ý tưởng giải
Đọc số bộ test
TVới mỗi bộ:
Gán
tong_tien = MLặp
ntháng:tong_tien *= (1 + r/100)
In kết quả định dạng 1 chữ số thập phân
🔹 Độ phức tạp
Mỗi test: O(n) (n ≤ 500)
Tổng: O(T × n) → chạy rất nhanh
⚠️ Lưu ý quan trọng khi thi
✔ Dùng số thực (float)
✔ Không làm tròn sớm
✔ Chỉ làm tròn khi in kết quả
✔ In đúng 1 chữ số thập phân
🧠 Vì sao KHÔNG dùng công thức mũ?
Có thể dùng:
❌ Nhưng dễ sai số số thực
✅ Vòng lặp an toàn hơn – đúng tinh thần đề THCS
📌 Tóm tắt nhanh
| Nội dung | Ghi nhớ |
|---|---|
| Loại lãi | Lãi kép |
| Công thức | Nhân dồn từng tháng |
| Output | 1 chữ số thập phân |
| Sai lầm hay gặp | Làm tròn sớm |